Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 3
Cours 3
Propriétés supplémentaires
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASomme et produit de racines
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorème
Si le trinôme a x^{2}+b x+c admet deux racines distinctes ou confondues, alors leur
somme \text{S} et leur produit \text{P} vérifient : \text{S}=\dfrac{-b}{a} et \text{P}=\dfrac{c}{a}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
Dans la première démonstration de la partie 2, on a établi que si x_1 et x_2 sont les racines d'un trinôme (éventuellement confondues), alors x_{1}+x_{2}=\dfrac{-b}{a} et x_{1} \times x_{2}=\dfrac{c}{a}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
Deux réels ont pour somme \text{S} et pour produit \text{P} si et seulement si ils sont solutions de l'équation x^{2}-\mathrm{S} x+\mathrm{P}=0.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Il s'agit d'une équivalence. Pour démontrer cette propriété, on montre un sens puis la réciproque.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
- Si deux réels x_1 et x_2 vérifient x_{1}+x_{2}=\mathrm{S} et x_{1} x_{2}=\mathrm{P}, alors : x_{2}=\mathrm{S}-x_{1} et \mathrm{P}=x_{1}\left(\mathrm{S}-x_{1}\right) et donc x_{1}^{2}-\mathrm{S} x_{1}+\mathrm{P}=0. Dans ce cas, x_1 est bien solution de x^{2}-\mathrm{S} x+\mathrm{P}. La démonstration est la même pour x_2.
- Réciproquement, si x_1 et x_2 sont solutions de x^{2}-\mathrm{S} x+\mathrm{P}=0, alors, d'après le théorème précédent, x_{1}+x_{2}=\dfrac{\mathrm{S}}{1}, soit x_{1}+x_{2}=\mathrm{S} et x_{1} x_{2}=\dfrac{\mathrm{P}}{1}, ainsi x_{1} x_{2} \: = \: \mathrm{P}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
L'équation 2 x^{2}-x-1=0 admet x_{1}=1 comme solution évidente.
L'autre solution x_2 vérifie donc 1 \times x_{2}=\dfrac{-1}{2}. D'où x_{2}=\dfrac{-1}{2}.
L'autre solution x_2 vérifie donc 1 \times x_{2}=\dfrac{-1}{2}. D'où x_{2}=\dfrac{-1}{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On parle de solution évidente lorsqu'un réel « simple‑» est solution de l'équation considérée. On teste quelques nombres comme 0 ; 1 ; -1 ; 2 et -2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Trouver, s'ils existent, deux nombres réels dont la somme est 4 et le produit 1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
- On utilise la propriété du cours. Les deux nombres, s'ils existent, sont solutions de l'équation x^{2}-4 x+1=0.
- On résout l'équation.
- Les solutions, si elles existent, sont les nombres recherchés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
S'ils existent, ces deux nombres sont solutions de l'équation x^{2}-4 x+1=0.
On a \Delta=12. \Delta>0 donc l'équation admet deux solutions réelles distinctes :
x_{1}=\dfrac{-(-4)-\sqrt{12}}{2} et x_{2}=\dfrac{-(-4)+\sqrt{12}}{2}.
Or \sqrt{12}=\sqrt{4 \times 3}=\sqrt{4} \times \sqrt{3}=2 \sqrt{3}.
Donc on a : x_{1}=\dfrac{4-2 \sqrt{3}}{2} et x_{2}=\dfrac{4+2 \sqrt{3}}{2}, soit {x_{1}=\dfrac{2(2-\sqrt{3})}{2}} et {x_{2}=\dfrac{2(2+\sqrt{3})}{2}}.
Ainsi x_{1}=2-\sqrt{3} et x_{2}=2+\sqrt{3}.
Les nombres recherchés sont 2-\sqrt{3} et 2+\sqrt{3}.
On a \Delta=12. \Delta>0 donc l'équation admet deux solutions réelles distinctes :
x_{1}=\dfrac{-(-4)-\sqrt{12}}{2} et x_{2}=\dfrac{-(-4)+\sqrt{12}}{2}.
Or \sqrt{12}=\sqrt{4 \times 3}=\sqrt{4} \times \sqrt{3}=2 \sqrt{3}.
Donc on a : x_{1}=\dfrac{4-2 \sqrt{3}}{2} et x_{2}=\dfrac{4+2 \sqrt{3}}{2}, soit {x_{1}=\dfrac{2(2-\sqrt{3})}{2}} et {x_{2}=\dfrac{2(2+\sqrt{3})}{2}}.
Ainsi x_{1}=2-\sqrt{3} et x_{2}=2+\sqrt{3}.
Les nombres recherchés sont 2-\sqrt{3} et 2+\sqrt{3}.
Pour s'entraîner
Exercices et p. 87
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BDiscriminant et sommet de parabole
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Propriété
La courbe représentative d'une fonction trinôme définie sur \R par f(x)=a x^{2}+b x+c est une parabole de sommet \text{S} qui a pour coordonnées \left(\dfrac{-b}{2 a} \: ;-\dfrac{\Delta}{4 a}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Dans le chapitre 2, les coordonnées du sommet \text{S} sont données par (\alpha \: ; \beta). On a donc \alpha=\dfrac{-b}{2 a} et \beta=\dfrac{-\Delta}{4 a}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Démonstration
On a f(x)=a\left[\left(x+\dfrac{b}{2 a}\right)^{2}-\dfrac{\Delta}{4 a^{2}}\right].
Le sommet \text{S} de la parabole a pour abscisse \dfrac{-b}{2 a}.
On a f\left(-\dfrac{b}{2 a}\right)=a\left[\left(-\dfrac{b}{2 a}+\dfrac{b}{2 a}\right)^{2}-\dfrac{\Delta}{4 a^{2}}\right]
=a\left(-\dfrac{\Delta}{4 a^{2}}\right)=-\dfrac{\Delta}{4 a}.
Donc \text{S} a pour coordonnées \left(-\dfrac{b}{2 a} \: ;-\dfrac{\Delta}{4 a}\right).
Le sommet \text{S} de la parabole a pour abscisse \dfrac{-b}{2 a}.
On a f\left(-\dfrac{b}{2 a}\right)=a\left[\left(-\dfrac{b}{2 a}+\dfrac{b}{2 a}\right)^{2}-\dfrac{\Delta}{4 a^{2}}\right]
=a\left(-\dfrac{\Delta}{4 a^{2}}\right)=-\dfrac{\Delta}{4 a}.
Donc \text{S} a pour coordonnées \left(-\dfrac{b}{2 a} \: ;-\dfrac{\Delta}{4 a}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemple
Soit f la fonction trinôme définie par f(x)=3 x^{2}-9 x+8.
On a \dfrac{-b}{2 a}=-\left(\dfrac{-9}{6}\right), soit \dfrac{-b}{2 a}=\dfrac{3}{2} et \Delta=-15.
Donc \dfrac{-\Delta}{4 a}=\dfrac{15}{12}, soit \dfrac{-\Delta}{4 a}=\dfrac{5}{4}.
Ainsi, le sommet \text{S} de la parabole représentant f a pour coordonnées \left(\dfrac{3}{2} \: ; \dfrac{5}{4}\right).
On a \dfrac{-b}{2 a}=-\left(\dfrac{-9}{6}\right), soit \dfrac{-b}{2 a}=\dfrac{3}{2} et \Delta=-15.
Donc \dfrac{-\Delta}{4 a}=\dfrac{15}{12}, soit \dfrac{-\Delta}{4 a}=\dfrac{5}{4}.
Ainsi, le sommet \text{S} de la parabole représentant f a pour coordonnées \left(\dfrac{3}{2} \: ; \dfrac{5}{4}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Application et méthode
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dresser le tableau de variations de la fonction f définie sur \R par f(x)=2 x^{2}-2 x+3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. On détermine les coordonnées du sommet de la parabole.
2. On regarde le signe de a pour déterminer le sens de variation de f.
3. On dresse le tableau de variations.
2. On regarde le signe de a pour déterminer le sens de variation de f.
3. On dresse le tableau de variations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Solution
Ici a = 2 , b = -2 et c = 3. On a \dfrac{-b}{2 a}=\dfrac{1}{2} et \Delta=-20.
Donc \dfrac{-\Delta}{4 a}=-\left(\dfrac{-20}{8}\right)=\dfrac{5}{2}.
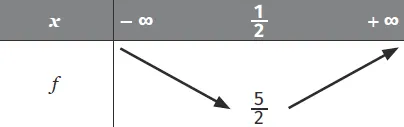
Par conséquent, f est représentée par une parabole de sommet \text{S}\left(\dfrac{1}{2} \: ; \dfrac{5}{2}\right).
Étant donné que a>0, voici le tableau de variations de f.
Donc \dfrac{-\Delta}{4 a}=-\left(\dfrac{-20}{8}\right)=\dfrac{5}{2}.
Par conséquent, f est représentée par une parabole de sommet \text{S}\left(\dfrac{1}{2} \: ; \dfrac{5}{2}\right).
Étant donné que a>0, voici le tableau de variations de f.
Le zoom est accessible dans la version Premium.
Pour s'entraîner
Exercices p. 87 ; et et p. 93
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah