Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 3
TP / TICE 2
Méthode de Hörner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Soient \text{P} un polynôme quelconque et \alpha un réel. L'algorithme de Hörner (ou schéma de Hörner) est un algorithme permettant de calculer \text{P}(\alpha) avec un nombre d'opérations réduit par rapport à la méthode classique. Dans le cas où \alpha est une racine du polynôme \text{P}, les coefficients obtenus, appelés coefficients de Hörner, permettent de factoriser \text{P}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Question préliminaire
On suppose que \text{P} est un polynôme de degré 3 et on note \mathrm{P}(x)=a_{3} x^{3}+a_{2} x^{2}+a_{1} x+a_{0} où a_{3}, a_{2}, a_{1} et a_{0} sont des réels tels que a_{3} \neq 0.
1. Démontrer que \mathrm{P}(\alpha)=a_{0}+\alpha\left[a_{1}+\alpha\left(a_{2}+\alpha a_{3}\right)\right]. L'algorithme décrit par la figure permet donc de calculer \mathrm{P}(\alpha).
2. Montrer que si \alpha est une racine de \text{P}, alors
\mathrm{P}(x)=(x-\alpha)\left[\textcolor{orange}{a_{3}} x^{2}+\left(\textcolor{orange}{a_{2}+\alpha a_{3}}\right) x+\textcolor{orange}{a_{1}+\alpha\left(a_{2}+\alpha a_{3}\right)}\right].
Les coefficients de Hörner sont donc a_{3} \: ; a_{2}+\alpha a_{3} \: ; a_{1}+\alpha\left(a_{2}+\alpha a_{3}\right).
1. Démontrer que \mathrm{P}(\alpha)=a_{0}+\alpha\left[a_{1}+\alpha\left(a_{2}+\alpha a_{3}\right)\right]. L'algorithme décrit par la figure permet donc de calculer \mathrm{P}(\alpha).
2. Montrer que si \alpha est une racine de \text{P}, alors
\mathrm{P}(x)=(x-\alpha)\left[\textcolor{orange}{a_{3}} x^{2}+\left(\textcolor{orange}{a_{2}+\alpha a_{3}}\right) x+\textcolor{orange}{a_{1}+\alpha\left(a_{2}+\alpha a_{3}\right)}\right].
Les coefficients de Hörner sont donc a_{3} \: ; a_{2}+\alpha a_{3} \: ; a_{1}+\alpha\left(a_{2}+\alpha a_{3}\right).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Découvrir la méthode de Hörner pour factoriser un polynôme dont on connaît une racine en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Python
1. Programmer dans la console ci-dessous, à l'aide de Python, l'algorithme de Hörner pour calculer \mathrm{P}(\alpha) où \text{P} est un polynôme de degré 3 donné et \alpha un réel donné.
2. Utiliser l'algorithme de Hörner pour calculer l'image
de 1, -3 et \sqrt{2} par les polynômes suivants :
• \text{P}_{1}(x)=x^{3}-2 x^{2}-x+1
• \text{P}_{2}(x)=-2 x^{3}+x^{2}-3 x-3
• \mathrm{P}_{3}(x)=x^{3}+x^{2}-3 x+1
3. Comment modifier cet algorithme pour obtenir les coefficients de Hörner lorsque \alpha est une racine de \text{P} ?
4. Utiliser l'algorithme modifié pour obtenir à la main une factorisation de \mathrm{P}_{3}.
5. Déterminer toutes les racines de \mathrm{P}_{3}.
• \text{P}_{1}(x)=x^{3}-2 x^{2}-x+1
• \text{P}_{2}(x)=-2 x^{3}+x^{2}-3 x-3
• \mathrm{P}_{3}(x)=x^{3}+x^{2}-3 x+1
3. Comment modifier cet algorithme pour obtenir les coefficients de Hörner lorsque \alpha est une racine de \text{P} ?
4. Utiliser l'algorithme modifié pour obtenir à la main une factorisation de \mathrm{P}_{3}.
5. Déterminer toutes les racines de \mathrm{P}_{3}.
Aide
La fonction créée prend comme arguments les
coefficients de \text{P} et \alpha.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On considère un polynôme \text{P} défini par \mathrm{P}(x)=x^{3}-2 x^{2}-x+1. Il s'agit d'utiliser un tableur pour calculer les coefficients de Hörner et pour calculer \mathrm{P}(\alpha) pour un \alpha donné.

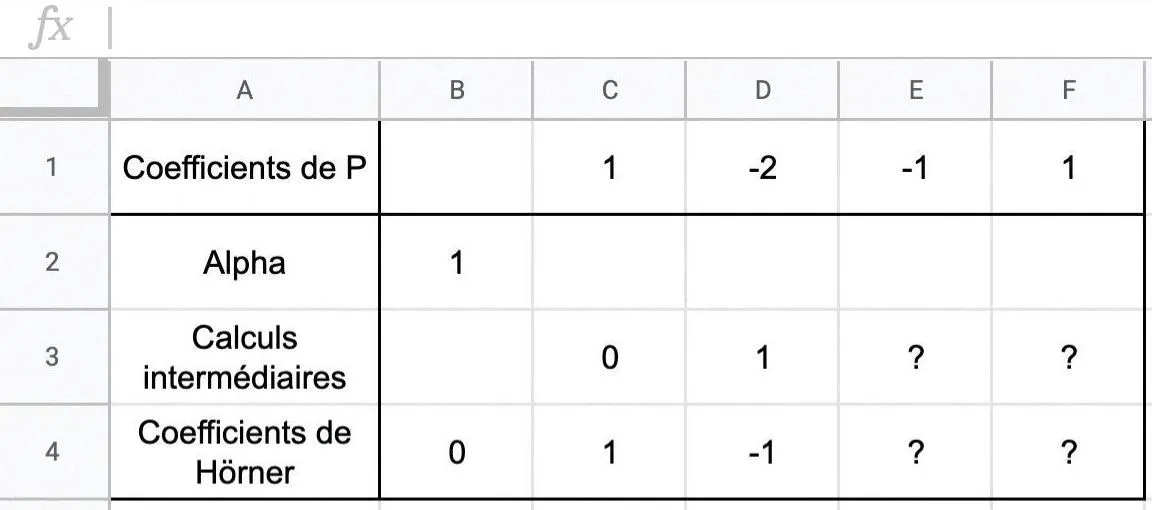
Une ligne du tableur contiendra les coefficients de \text{P}. Une cellule à part contiendra la valeur de \alpha. Sur une ligne devront apparaître les calculs intermédiaires en commençant par la valeur 0 pour initialiser le processus.
Une autre ligne contiendra les coefficients de Hörner (on pourra commencer également par la valeur 0) et la dernière cellule de cette ligne contiendra \mathrm{P}(\alpha).


Une autre ligne contiendra les coefficients de Hörner (on pourra commencer également par la valeur 0) et la dernière cellule de cette ligne contiendra \mathrm{P}(\alpha).
1. Déterminer les formules à entrer dans les lignes 3 et 4 pour obtenir les résultats voulus en étirant les formules vers la droite, puis entrez-les dans le tableur. Où lit-on \mathrm{P}(\alpha) \: ?
2. Utiliser la feuille de calcul pour calculer l'image de 1, -3 et \sqrt{2} par les polynômes suivants :
• \text{P}_{1}(x)=x^{3}-2 x^{2}-x+1
• \text{P}_{2}(x)=-2 x^{3}+x^{2}-3 x-3
• \mathrm{P}_{3}(x)=x^{3}+x^{2}-3 x+1
3. Donner une racine du polynôme \text{P}_3.
4. Utiliser les coefficients de Hörner donnés par la feuille de calcul pour obtenir une factorisation de \text{P}_3 puis déterminer toutes les racines de \text{P}_3.
2. Utiliser la feuille de calcul pour calculer l'image de 1, -3 et \sqrt{2} par les polynômes suivants :
• \text{P}_{1}(x)=x^{3}-2 x^{2}-x+1
• \text{P}_{2}(x)=-2 x^{3}+x^{2}-3 x-3
• \mathrm{P}_{3}(x)=x^{3}+x^{2}-3 x+1
3. Donner une racine du polynôme \text{P}_3.
4. Utiliser les coefficients de Hörner donnés par la feuille de calcul pour obtenir une factorisation de \text{P}_3 puis déterminer toutes les racines de \text{P}_3.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
