Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 3
Entraînement 2
Factorisation et signe du trinôme
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Calculer.] On pose \mathrm{A}(x)=\dfrac{x+1}{x^{2}-3 x-4}. 1. Déterminer les racines de x^{2}-3 x-4.
2. Factoriser x^{2}-3 x-4.
3. Après avoir précisé l'ensemble des réels x pour lesquels \text{A}(x) existe, simplifier l'écriture de \text{A}(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Calculer.]
On considère la fraction rationnelle suivante :
f(x)=\dfrac{2-x}{-3 x^{2}+11 x-10} 1. Donner l'ensemble de définition de f.
2. Factoriser le dénominateur puis simplifier l'écriture de f(x).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Calculer.]
Reprendre l'exercice précédent avec les fractions rationnelles suivantes. 1. g(x)=\dfrac{9 x^{2}-16}{9 x^{2}-9 x-4}
2. h(x)=\dfrac{x^{2}-7 x-18}{5 x^{2}+3 x-14}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
[Représenter.]
On a obtenu la courbe de la fonction f sur l'écran de la calculatrice.

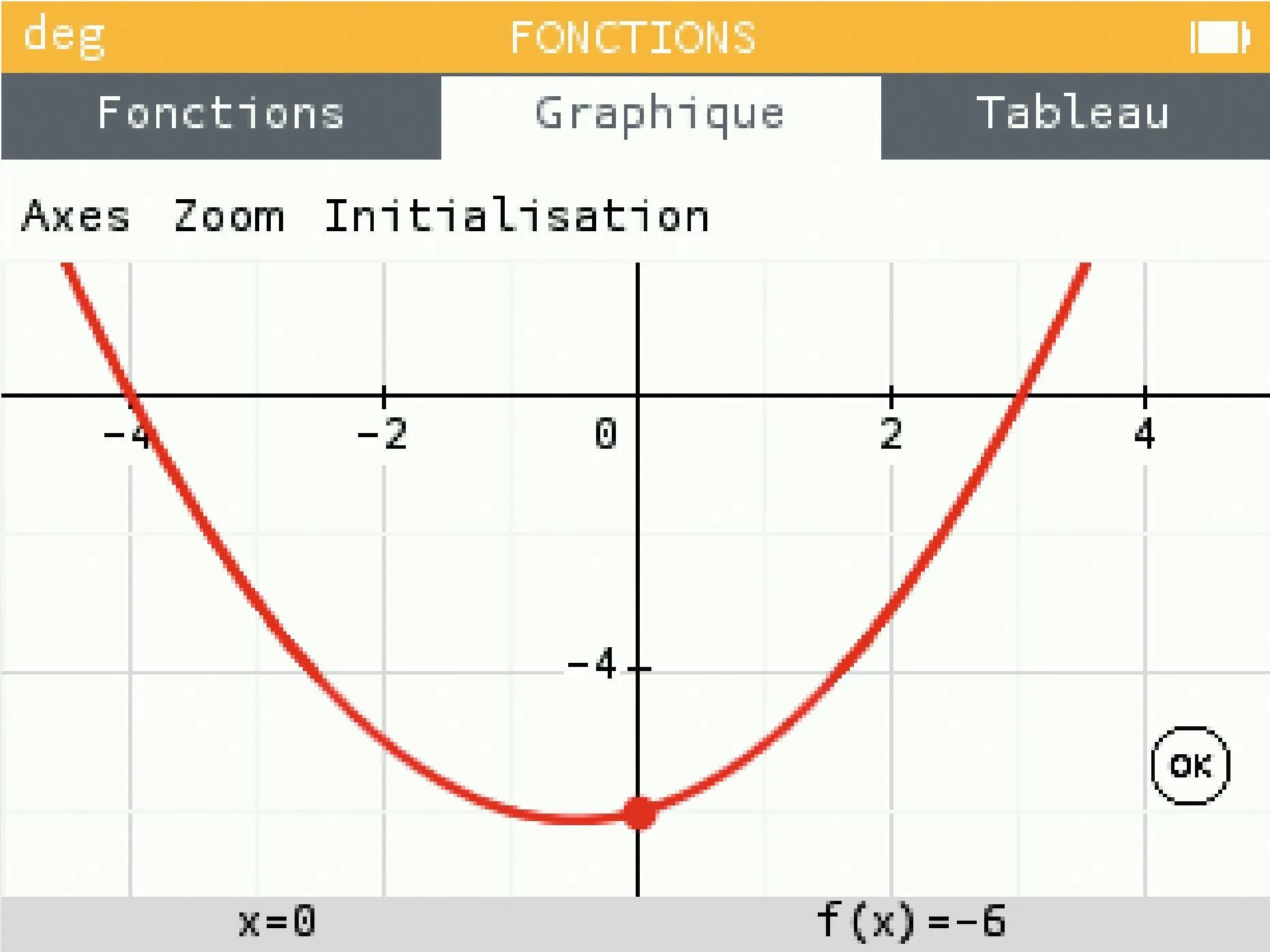
1. Par lecture graphique, donner les solutions entières de l'équation f(x) =0.
2. En utilisant l'autre information disponible sur l'écran, déterminer f(x) en fonction de x.
2. En utilisant l'autre information disponible sur l'écran, déterminer f(x) en fonction de x.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
[Calculer.] On cherche à résoudre l'équation (\text{E}) suivante.
x^{3}+5 x^{2}-x-5=0. Pour tout x \in \mathbb{R}, on pose \mathrm{A}(x)=x^{3}+5 x^{2}-x-5. 1. Montrer que, pour tout x \in \R,
\mathrm{A}(x)=(x+1)^{3}+2\left(x^{2}-2 x-3\right).
2. Pour tout x \in \R, on pose \mathrm{B}(x)=x^{2}-2 x-3.
Factoriser \mathrm{B}(x).
3. En utilisant les questions 1. et 2., résoudre l'équation (\text{E}).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Résoudre les inéquations suivantes dans \R.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
66
[Calculer.] 1. x^{2}-3 x+1\lt0
2. 2 x^{2}+5 x-7 \geqslant 0
3. 9 x^{2}+12 x+4>0
4. 3 x^{2}-x+1 \leqslant 0
5. -x^{2}+5 x-7\lt0
6. -4 x^{2}+20 x-25 \geqslant 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
67
[Calculer.]
1. 2 x^{2}-4 \geqslant 0
2. x^{2}+1\lt0
3. -5 x^{2}>(-3 x+1)(x+2)
4. -x^{2}-5 x \leqslant 0
5. (x-1)\left(x^{2}+3\right)>(x+1)(5 x-3)
6. 4(x-3)^{2} \geqslant(7+4 x)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
68
[Calculer.]
1. -x^{2}-4>0
2. 16+(x-1)^{2}\lt0
3. (2 x-5)^{2} \geqslant 9
4. -4 x^{2}+48 \leqslant 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
70
[Calculer.]
1. \left(-3 x^{2}-2 x+8\right)\left(5 x^{2}+2 x-3\right) \geqslant 0
2. \left(x^{2}+3 x-4\right)\left(3 x^{2}-5 x+2\right) \geqslant 0
3. \left(-x^{2}+2 x-1\right)\left(2 x^{2}-x-6\right)\lt0
4. \left(-x^{2}+x-7\right)\left(3 x^{2}-x+2\right) \geqslant 0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
69
[Calculer.]
1. \left(-3 x^{2}+x+2\right)(x+3) \geqslant 0
2. \left(5 x^{2}-x+3\right)(3-2 x)\lt0
3. (3 x-1)\left(2 x^{2}+3 x-5\right)>0
4. (x-2)\left(-x^{2}+x-2\right) \leqslant 0
5. \left(5 x^{2}+3 x-2\right)(x+1)>0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
71
[Calculer.] Déterminer les valeurs de x pour lesquelles les encadrements suivants sont vérifiés. 1. -3 \leqslant x^{2}-2 x-15 \leqslant 1
2. 2\lt\dfrac{3 x^{2}+1}{-x+7}\lt7
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
72
[Calculer.] Résoudre les inéquations suivantes après avoir donné l'ensemble de résolution.
1. x^{3}-4 x^{2}+x \geqslant 0
2. \dfrac{3 x^{2}+x-2}{x-2}\lt0
3. \dfrac{-2 x^{2}-5 x+3}{x^{2}-4 x-5}\lt0
2. \dfrac{3 x^{2}+x-2}{x-2}\lt0
3. \dfrac{-2 x^{2}-5 x+3}{x^{2}-4 x-5}\lt0
4. \dfrac{x^{2}+x+1}{2 x^{2}-5 x+7}\lt0
5. \dfrac{-x+4}{3 x-5} \geqslant \dfrac{2 x-1}{4 x+5}
6. 1+\dfrac{2}{3 x+1}\lt\dfrac{1}{x-5}
5. \dfrac{-x+4}{3 x-5} \geqslant \dfrac{2 x-1}{4 x+5}
6. 1+\dfrac{2}{3 x+1}\lt\dfrac{1}{x-5}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
73
[Calculer.]
Donner le domaine de définition des fonctions suivantes.
1. f : x \mapsto \sqrt{x^{2}+4 x-5}
2. g : x \mapsto \dfrac{3}{x \sqrt{7 x^{2}-2 x-5}}
2. g : x \mapsto \dfrac{3}{x \sqrt{7 x^{2}-2 x-5}}
3. h : x \mapsto \sqrt{\dfrac{x}{3 x^{2}-13 x+4}}
4. l : x \mapsto \sqrt{x^{2}-3 x-10}+\sqrt{x}
4. l : x \mapsto \sqrt{x^{2}-3 x-10}+\sqrt{x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
74
En SVT
[Modéliser.]
D'après Bac ES - Polynésie - 2014
On étudie la concentration dans le sang en fonction du temps d'un antibiotique injecté en une seule prise à un patient. On modélise cette concentration par la fonction g définie sur l'intervalle [0 \: ; 10] par g(t)=\dfrac{4 t}{t^{2}+1}.
g(t) représente la concentration en mg·L-1 de l'antibiotique lorsque t heures se sont écoulées. Répondre aux questions suivantes de façon algébrique puis vérifier à l'aide d'un graphique à la calculatrice. 1. Dans quel intervalle de temps la concentration sera-t-elle supérieure ou égale à 1,6 mg·L-1 ?
2. La concentration peut-elle être strictement supérieure à 2 mg·L-1 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
75
[Chercher.]
Un miroir peut être représenté par la figure ci-dessous. Le rectangle \text{ABCD} symbolise le cadre du miroir. \text{AEFD} est un trapèze et constitue le miroir proprement dit. Les deux triangles \text{ABE} et \text{DFC} sont des pièces de bois ouvragées.
L'unité est le centimètre. On pose \mathrm{EF}=x et on a \mathrm{BE}=\mathrm{FC}, \mathrm{AB}=x+20 et \mathrm{AD}=30.
L'unité est le centimètre. On pose \mathrm{EF}=x et on a \mathrm{BE}=\mathrm{FC}, \mathrm{AB}=x+20 et \mathrm{AD}=30.

Quelle est la valeur minimale à donner à x pour que le miroir \text{AEFD} ait une aire supérieure aux neuf dixièmes de l'aire totale de \text{ABCD} \: ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
76
[Chercher.]
Soit \mathcal{P} la courbe d'équation y=x^{2} et \mathcal{D} la droite d'équation y=\dfrac{1}{2} x+\dfrac{1}{2}. Étudier la position relative de ces deux courbes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
77
En physique
[Modéliser.]
Lors d'un freinage d'urgence, la distance que parcourt le véhicule avant l'arrêt total se décompose en deux parties : la distance parcourue pendant le temps de réaction du conducteur et la distance de freinage parcourue au cours du freinage du véhicule. 1. Le temps de réaction du conducteur, c'est-à-dire le temps nécessaire pour prendre conscience de la situation et appuyer sur le frein, est d'environ une seconde.
Si on appelle v la vitesse du véhicule en km·h–1, montrer que la distance d_r, en mètre, parcourue pendant ce temps de réaction vérifie : {d_{r}=\dfrac{v}{3{,}6}.}
2. Pour la distance de freinage d_f, exprimée en mètre, on donne la formule suivante {d_{f}=\dfrac{v^{2}}{200}.}
La distance d'arrêt est donc égale à {d_{a}=d_{r}+d_{f}.}
Une voiture roule à 110 km·h–1. Quelle est sa distance d'arrêt (on arrondira au centième près) ?
3. Quelles sont les vitesses qui permettent de s'arrêter en moins de 15 m ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
78
Démo
[Raisonner.]
Soient a , b , c et d quatre réels tels que a \neq 0. On note \text{P} le polynôme de degré 3 défini par \mathrm{P}(x)=a x^{3}+b x^{2}+c x+d. 1. Démontrer que, pour tous réels x et \alpha,
x^{3}-\alpha^{3}=(x-\alpha)\left(x^{2}+x \alpha+\alpha^{2}\right).
2. On suppose maintenant que \alpha est une racine de \text{P}.
a. Justifier que l'on peut écrire, pour tout {x \in \R}, \mathrm{P}(x)=\mathrm{P}(x)-\mathrm{P}(\alpha).
b. En déduire alors que, pour tout réel x,
\mathrm{P}(x)=a\left(x^{3}-\alpha^{3}\right)+b\left(x^{2}-\alpha^{2}\right)+c(x-\alpha).
3. Justifier alors que \text{P}(x) est factorisable par (x - \alpha) et donner cette factorisation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
79
[Calculer.]
Pour chacun des polynômes suivants :
- vérifier que 1 est une racine ;
- factoriser le polynôme par x - 1 en utilisant l'exercice précédent ;
- déterminer toutes les racines du polynôme.
2. \mathrm{P}_{2}(x)=x^{3}-9 x^{2}+24 x-16
3. \mathrm{P}_{3}(x)=4 x^{3}+8 x^{2}-2 x-10
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
