Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 6
TP / TICE 2
Évolution du nombre de noyaux radioactifs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Certaines proportions de protons et neutrons dans le noyau d'un atome ne permettent pas la stabilité du noyau.
Le noyau est alors dit radioactif. Les noyaux instables se désintègrent spontanément mais on ne peut prévoir à
quel instant. Néanmoins, sur des échantillons comportant de très nombreux noyaux radioactifs, la courbe traduisant
le nombre de noyaux radioactifs en fonction du temps a toujours la même allure.
On admet que la fonction \mathrm{N} : t \mapsto \mathrm{N}_{0} \exp \left(-\dfrac{t}{\tau}\right) où \mathrm{N}_{0} est le nombre de noyaux radioactifs à l'instant initial t = 0 et \tau est une constante (appelée constante de temps) caractéristique du noyau radioactif étudié donne l'évolution du nombre de noyaux radioactifs en fonction du temps.
On appelle demi-vie d'un échantillon radioactif la durée au bout de laquelle le nombre de noyaux est divisé par deux par rapport au nombre de noyaux initial. Cette modélisation est vraie pour \mathrm{N}_{0} très grand. Dans le cadre de cet exercice, on se limitera à des valeurs plus raisonnables pour les logiciels.
On donne les caractéristiques suivantes pour des atomes particuliers.
On admet que la fonction \mathrm{N} : t \mapsto \mathrm{N}_{0} \exp \left(-\dfrac{t}{\tau}\right) où \mathrm{N}_{0} est le nombre de noyaux radioactifs à l'instant initial t = 0 et \tau est une constante (appelée constante de temps) caractéristique du noyau radioactif étudié donne l'évolution du nombre de noyaux radioactifs en fonction du temps.
On appelle demi-vie d'un échantillon radioactif la durée au bout de laquelle le nombre de noyaux est divisé par deux par rapport au nombre de noyaux initial. Cette modélisation est vraie pour \mathrm{N}_{0} très grand. Dans le cadre de cet exercice, on se limitera à des valeurs plus raisonnables pour les logiciels.
On donne les caractéristiques suivantes pour des atomes particuliers.
| \mathrm{N}_{0} | \tau | Unité de temps | |
| Polonium 210 | 5 000 | 199,6 | jour |
| Iode 131 | 10 000 | 11,57 | jour |
| Uranium 235 | 1 000 | 1 015 | million d'années |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions préliminaires
1. La courbe ci-contre traduit l'évolution de noyaux radioactifs
d'uranium 235. Estimer une valeur approchée de la demi-vie de cet atome.
2. Quelle est l'expression de la fonction \mathrm{N}(t) associée à cet échantillon d'uranium ?
2. Quelle est l'expression de la fonction \mathrm{N}(t) associée à cet échantillon d'uranium ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Déterminer la constante de temps \tau de différents noyaux radioactifs à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. Tracer les courbes correspondant aux trois
atomes étudiés dans GeoGebra.
2. Rechercher graphiquement les demi-vies de
chaque noyau radioactif. Il peut être utile de régler
l'échelle des axes pour faciliter la lecture.
3. Tracer les tangentes à chacune des courbes au point d'abscisse 0.
4. Relever l'abscisse du point d'intersection des tangentes avec l'axe des abscisses que l'on notera x_{0}.
5. Quel lien peut-on faire entre \tau et x_{0} pour chaque échantillon ?
6. Pour chaque noyau, diviser la demi-vie par l'abscisse du point x_{0} .
7. Que peut-on en déduire ?
3. Tracer les tangentes à chacune des courbes au point d'abscisse 0.
4. Relever l'abscisse du point d'intersection des tangentes avec l'axe des abscisses que l'on notera x_{0}.
5. Quel lien peut-on faire entre \tau et x_{0} pour chaque échantillon ?
6. Pour chaque noyau, diviser la demi-vie par l'abscisse du point x_{0} .
7. Que peut-on en déduire ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
On souhaite utiliser un tableur pour déterminer la
demi-vie du polonium, de l'iode et de l'uranium.
1. Recopier le tableau suivant. Pourquoi utilise-t-on le signe $ ?

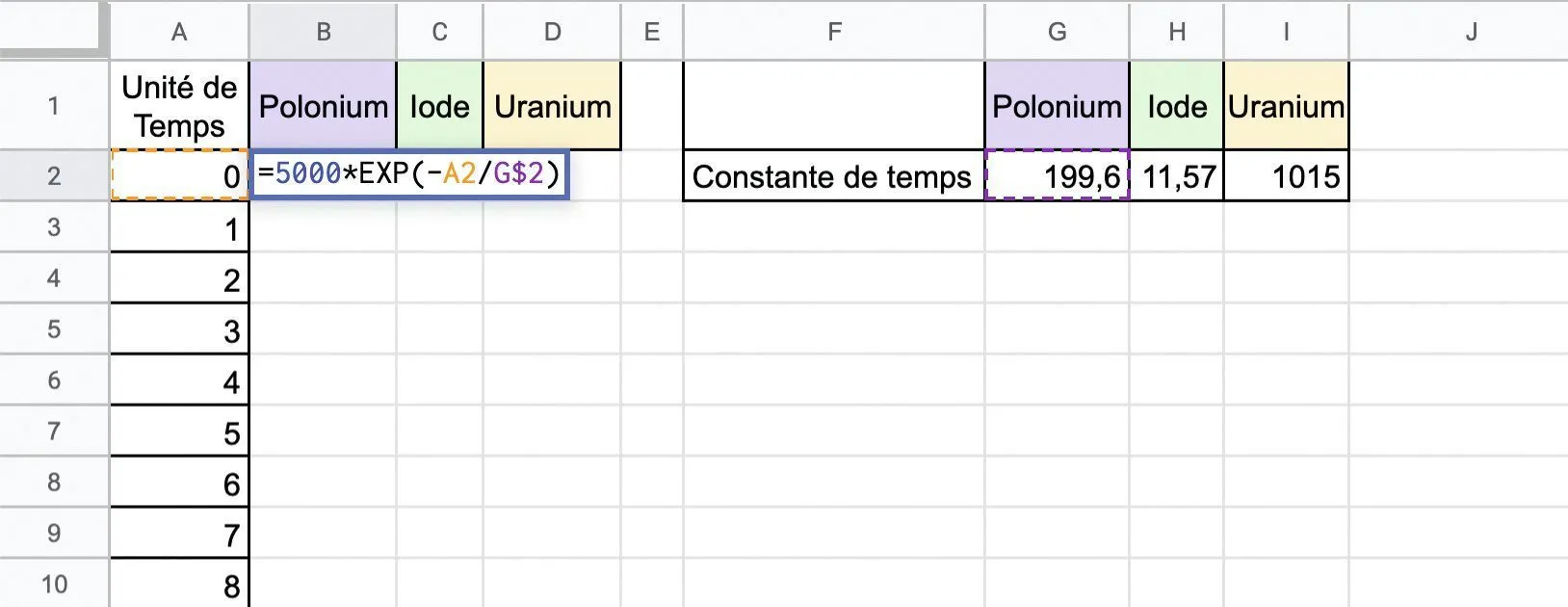
2. Étirer la formule vers le bas jusqu'à trouver un encadrement à l'unité près de la demi-vie du polonium. Dans la case G3, inscrire la borne supérieure.


2. Étirer la formule vers le bas jusqu'à trouver un encadrement à l'unité près de la demi-vie du polonium. Dans la case G3, inscrire la borne supérieure.
3. Procéder de la même façon pour trouver un encadrement à l'unité près des demi-vies de l'iode et de l'uranium. Inscrire les bornes supérieures des intervalles dans les cases H3 et I3.
4. Dans les cases G4, H4 et I4, calculer le rapport de la demi-vie par la constante \tau. Que remarque-t-on ?
5. Comment faire pour obtenir une estimation plus précise du temps de demi-vie ?
4. Dans les cases G4, H4 et I4, calculer le rapport de la demi-vie par la constante \tau. Que remarque-t-on ?
5. Comment faire pour obtenir une estimation plus précise du temps de demi-vie ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
