Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 6
Entraînement
Généralités sur la fonction exponentielle
9 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
45
[Calculer.] f est définie sur \R par {f(x)=-2\, \mathrm{e}^{x}.}
Vérifier que f = f' et calculer f(0).
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
[Calculer.]
Déterminer une fonction g définie et dérivable sur \mathbb{R} telle que g' = g et g(0)=\dfrac{3}{2}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
[Calculer.]
Déterminer une fonction h définie et dérivable sur \mathbb{R} telle que h' = h et h(0)=-4.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
Démo
[Raisonner.]
On souhaite démontrer que, pour tous réels x et y, \mathrm{e}^{x-y}=\dfrac{\mathrm{e}^{x}}{\mathrm{e}^{y}}. 1. Écrire \dfrac{\mathrm{e}^{x}}{\mathrm{e}^{y}} sous la forme d'un produit.
2. Sachant que \mathrm{e}^{x} \times \mathrm{e}^{y}=\mathrm{e}^{x+y} et \mathrm{e}^{-x}=\dfrac{1}{\mathrm{e}^{x}}, démontrer la proposition énoncée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Calculer.]
Simplifier au maximum les expressions suivantes ; c'est-à-dire en n'utilisant qu'une seule fois l'exponentielle dans l'expression finale.
1. \mathrm{A}=\mathrm{e}^{5} \times\left(\mathrm{e}^{3}\right) \times \mathrm{e}^{-4}
2. \mathrm{B}=\dfrac{\mathrm{e}^{7}}{\mathrm{e}^{-4}}
3. \mathrm{C}=\dfrac{\mathrm{e}^{-3} \times \mathrm{e}^{8}}{\mathrm{e}^{3}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
50
[Calculer.] Simplifier au maximum les expressions suivantes. 1. \mathrm{A}=\mathrm{e}^{2} \times \mathrm{e}^{32} \times \mathrm{e}^{8}
2. \mathrm{B}=\dfrac{\mathrm{e}}{\mathrm{e}^{5}}
3. \mathrm{C}=\dfrac{\left(\mathrm{e}^{7}\right)^{3} \times \mathrm{e}^{4}}{\mathrm{e}^{-4}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51
[Calculer.]
x est un réel quelconque. Simplifier au maximum les expressions suivantes.
1. a(x)=\mathrm{e}^{2 x} \times\left(\mathrm{e}^{x}\right)^{2} \times \mathrm{e}^{-3 x}
2. b(x)=\dfrac{\mathrm{e}^{x^{2}}}{\mathrm{e}^{x}}
2. b(x)=\dfrac{\mathrm{e}^{x^{2}}}{\mathrm{e}^{x}}
3. c(x)=\dfrac{\mathrm{e}^{x-1} \times \mathrm{e}^{4 x}}{\mathrm{e}^{x}}
4. d(x)=\dfrac{\mathrm{e}^{-2 x}}{\mathrm{e}^{-3 x} \times \mathrm{e}^{x+1}}
4. d(x)=\dfrac{\mathrm{e}^{-2 x}}{\mathrm{e}^{-3 x} \times \mathrm{e}^{x+1}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52
[Calculer.]
t est un réel quelconque. Simplifer au maximum les expressions suivantes. 1. d(t)=\mathrm{e}^{3 t} \times \mathrm{e}^{1-6 t} \times\left(\mathrm{e}^{2 t+1}\right)^{3}
2. e(t)=\dfrac{\mathrm{e}^{8 t-3}}{\mathrm{e}^{2 t+5}}
3. f(t)=\dfrac{\mathrm{e}^{-2 t+1} \times \mathrm{e}^{6 t+5}}{\mathrm{e}^{-4 t-2}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53
[Calculer.] n est un entier relatif quelconque. Simplifier au maximum les expressions suivantes. 1. u(n)=\mathrm{e}^{2 n+1} \times \mathrm{e}^{3 n-4}
2. v(n)=\dfrac{\mathrm{e}^{5 n-3}}{\mathrm{e}^{-2 n+1}}
3. w(n)=\left(\mathrm{e}^{2 n-1}\right)^{2} \times \mathrm{e}^{3 n+4}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
54
[Calculer.]
x est un réel quelconque. Simplifier au maximum les expressions suivantes. 1. g(x)=\left(\mathrm{e}^{4 x-5} \times \mathrm{e}^{3 x+2}\right)^{3}
2. h(x)=\dfrac{\mathrm{e}^{3 x}}{\mathrm{e}^{-x} \times\left(\mathrm{e}^{-3 x}\right)^{2}}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
55
[Calculer.]
Dans GeoGebra, la commande Simplifier permet
d'écrire une fonction sous la forme la plus simple
possible.
Le zoom est accessible dans la version Premium.
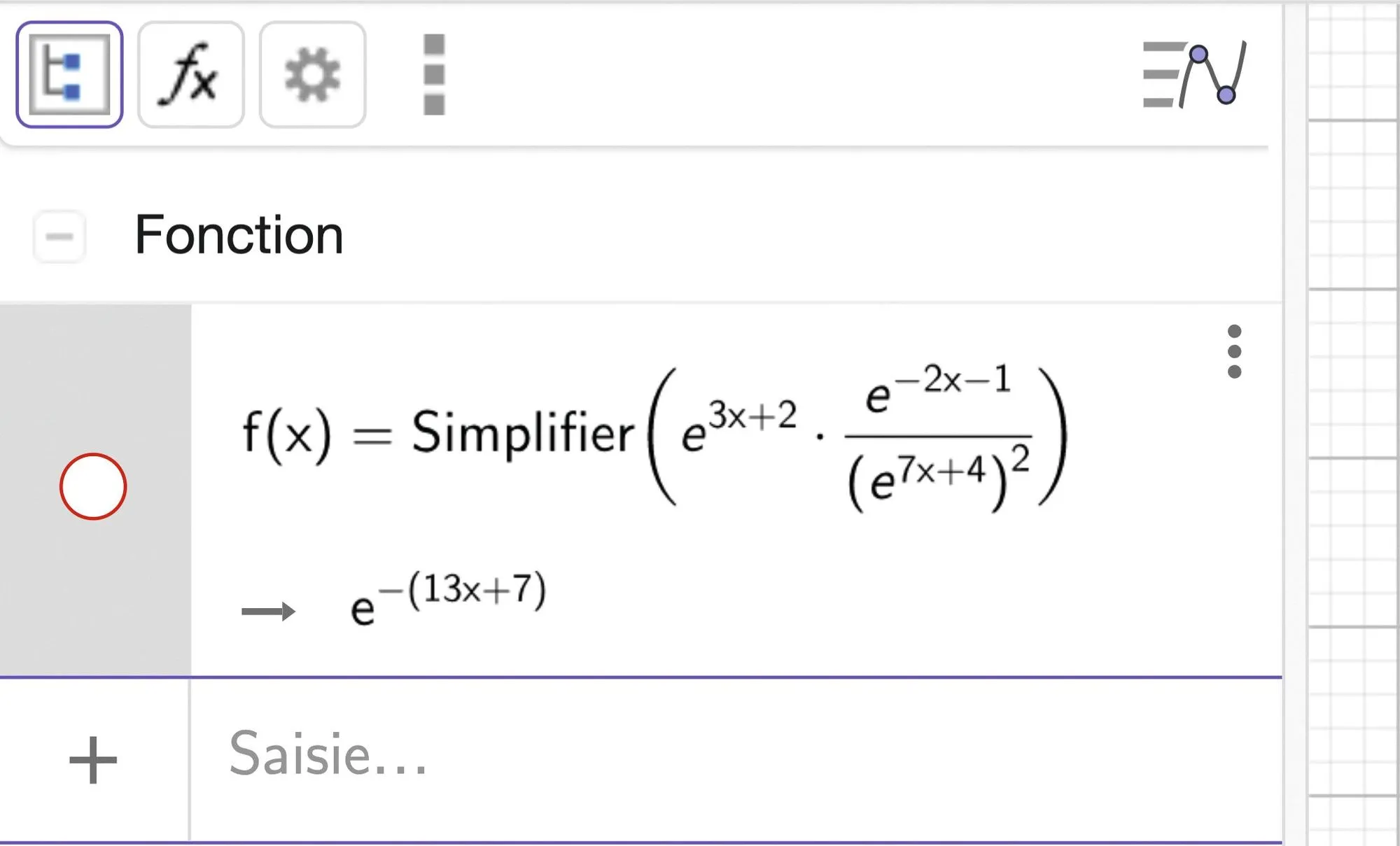
Vérifier que l'expression saisie se simplifie bien en \mathrm{e}^{-(13 x+7)}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
56
[Calculer.] Développer et réduire les expressions suivantes. 1. \mathrm{A}=\mathrm{e}^{4}\left(\mathrm{e}^{3}+\mathrm{e}^{7}\right)
2. \mathrm{B}=\left(\mathrm{e}^{2}+\mathrm{e}^{6}\right)\left(\mathrm{e}^{3}+\mathrm{e}\right)
3. \mathrm{C}=\left(\mathrm{e}^{8}-\mathrm{e}^{2}\right)\left(\mathrm{e}^{6}+1\right)
4. \mathrm{D}=\left(\mathrm{e}^{-2}+\mathrm{e}^{3}\right)\left(\mathrm{e}^{-2}-\mathrm{e}^{8}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
57
[Calculer.]
Développer et réduire les expressions suivantes. 1. \mathrm{A}=\left(\mathrm{e}^{3}+\mathrm{e}^{5}\right)^{2}
2. \mathrm{B}=\left(\mathrm{e}^{2}-\mathrm{e}^{-2}\right)^{2}
3. \mathrm{C}=\left(\mathrm{e}^{6}-\mathrm{e}^{-4}\right)\left(\mathrm{e}^{6}+\mathrm{e}^{-4}\right)
4. \mathrm{D}=\left(2 \, \mathrm{e}^{4}-3 \, \mathrm{e}^{-1}\right)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58
[Calculer.]
t est un réel quelconque. Développer et réduire les expressions suivantes. 1. \mathrm{A}(t)=\left(\mathrm{e}^{t}-1\right)\left(\mathrm{e}^{t}+1\right)
2. \mathrm{B}(t)=\left(\mathrm{e}^{t}+3\right)^{2}
3. \mathrm{C}(t)=\left(\mathrm{e}^{2 t}-2\right)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59
[Calculer.]
x est un réel quelconque. Développer et réduire les expressions suivantes. 1. \mathrm{D}(x)=\left(\mathrm{e}^{x}+\mathrm{e}^{-2 x}\right)^{2}
2. \mathrm{E}(x)=\left(\mathrm{e}^{3 x}-\mathrm{e}^{5 x}\right)^{2}
3. \mathrm{F}(x)=\left(\mathrm{e}^{-2 x}-\mathrm{e}^{x}\right)\left(\mathrm{e}^{-2 x}+\mathrm{e}^{x}\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60
[Calculer.]
x est un réel quelconque. Développer et réduire les expressions suivantes. 1. \mathrm{O}(x)=\left(\mathrm{e}^{x}+\mathrm{e}^{-x}\right)^{2}+\left(\mathrm{e}^{x}-\mathrm{e}^{-x}\right)^{2}
2. \mathrm{P}(x)=\left(\mathrm{e}^{x}+\mathrm{e}^{-x}\right)^{2}-\left(\mathrm{e}^{x}-\mathrm{e}^{-x}\right)^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61
[Calculer.] Démontrer les égalités suivantes pour tout réel x . 1. \dfrac{\mathrm{e}^{x}-1}{\mathrm{e}^{x}}=1-\mathrm{e}^{-x}
2. \dfrac{1}{\mathrm{e}^{x}+1}=\dfrac{\mathrm{e}^{x}-1}{\mathrm{e}^{2 x}-1}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62
[Calculer.]
Démontrer l'égalité suivante pour tout réel x .
\left(\mathrm{e}^{x}+\mathrm{e}^{-x}\right)\left(\mathrm{e}^{2 x}\right)^{2}=\mathrm{e}^{3 x}\left(\mathrm{e}^{2 x}+1\right)
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63
[Calculer.]
Soit x \in \mathbb{R}. Factoriser les expressions suivantes.
1. \mathrm{e}^{4 x}+\mathrm{e}^{x}
2. \mathrm{e}^{4 x}-1
2. \mathrm{e}^{4 x}-1
3. \mathrm{e}^{6 x}+4\, \mathrm{e}^{3 x}+4
4. 9\,\mathrm{e}^{-2 x}-6+\mathrm{e}^{2 x}
4. 9\,\mathrm{e}^{-2 x}-6+\mathrm{e}^{2 x}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64
Tableur
[Calculer.]
On considère les fonctions f et g définies sur \mathbb{R} par
{f(x)=\dfrac{\mathrm{e}^{2 x} \times \mathrm{e}^{3 x+2}}{\mathrm{e}^{-x}}} et {g(x)=\dfrac{\mathrm{e}^{4 x} \times \mathrm{e}^{3 x+5}}{\mathrm{e}^{x-1}}.}
On souhaite comparer ces deux fonctions à l'aide d'un tableur. Dans un tableur, la fonction exponentielle s'appelle EXP.
On souhaite comparer ces deux fonctions à l'aide d'un tableur. Dans un tableur, la fonction exponentielle s'appelle EXP.
Le zoom est accessible dans la version Premium.
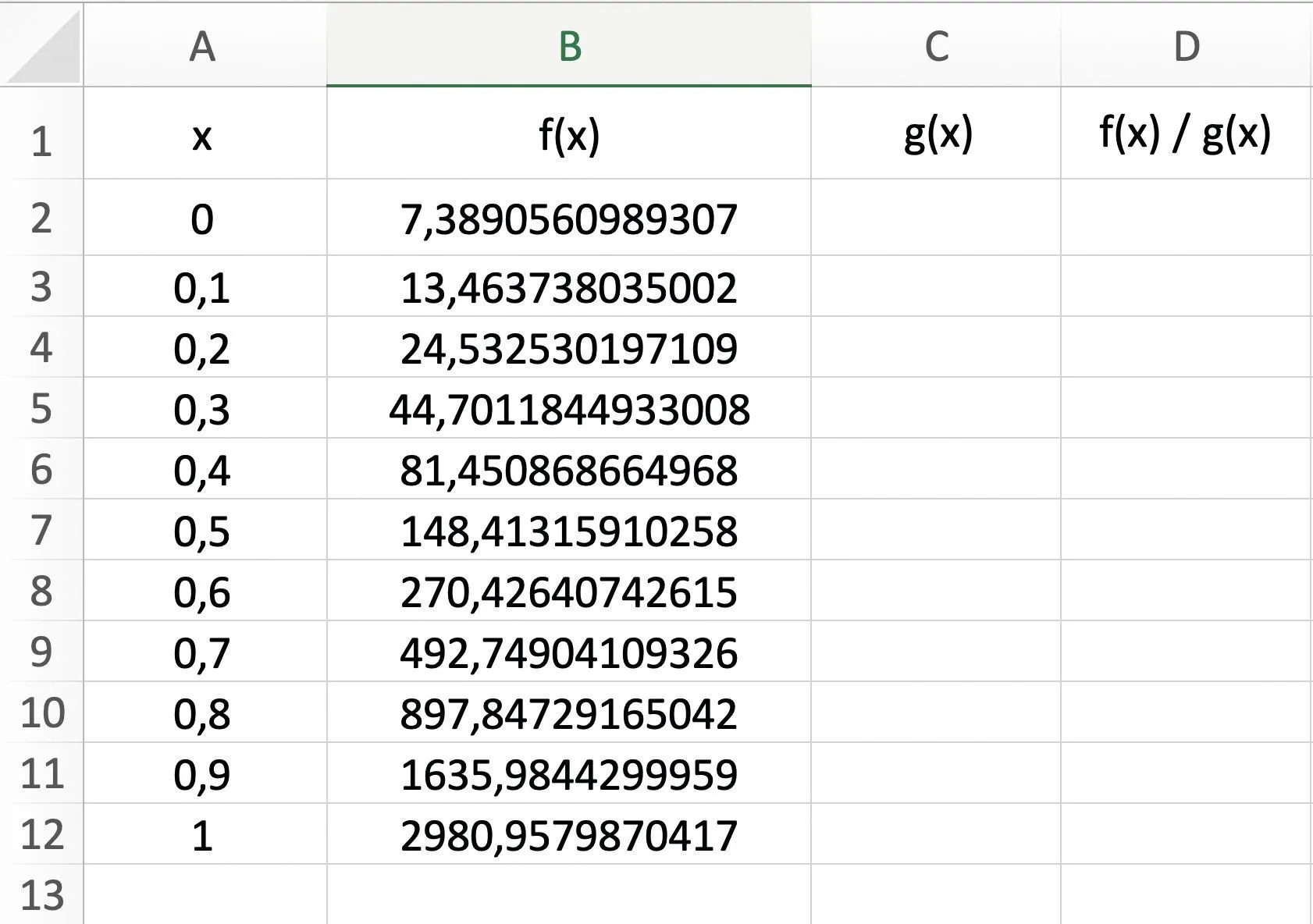
1. Quelle formule a-t-on entrée dans la case B2 avant de
l'étirer vers le bas pour obtenir les images par f des
nombres x de la colonne A ?
2. Faire de même avec les images par g dans la colonne C.
3. a. Démontrer que la fonction g ne s'annule jamais.
2. Faire de même avec les images par g dans la colonne C.
3. a. Démontrer que la fonction g ne s'annule jamais.
b. Dans la colonne D, calculer les rapports \dfrac{f(x)}{g(x)}. Que remarque-t-on ?
4. Démontrer cette conjecture par le calcul.
4. Démontrer cette conjecture par le calcul.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
65
Python
[Calculer.]
En Python, l'exponentielle fait partie de la librairie math. Pour pouvoir l'utiliser, il faut en première ligne du programme entrer l'instruction from math import exp.
1. Calculer à la main \mathrm{e}^{4}-\left(\mathrm{e}^{2}\right)^{2}.
2. Calculer et afficher \mathrm{e}^{4}-\left(\mathrm{e}^{2}\right)^{2} avec Python. Qu'obtient-on ? Pourquoi ?
2. Calculer et afficher \mathrm{e}^{4}-\left(\mathrm{e}^{2}\right)^{2} avec Python. Qu'obtient-on ? Pourquoi ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah