Physique-Chimie 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
1. Constitution et transformations de la matière
Ch. 1
Composition chimique d'un système
Ch. 2
Composition chimique des solutions
Ch. 3
Évolution d'un système chimique
Ch. 4
Réactions d'oxydoréduction
Ch. 5
Détermination d'une quantité de matière par titrage
Livret Bac : Thème 1
Ch. 6
De la structure à la polarité d'une entité
Ch. 7
Interpréter les propriétés d’une espèce chimique
Ch. 8
Structure des entités organiques
Ch. 9
Synthèse d'espèces chimiques organiques
Ch. 10
Conversions d'énergie au cours d'une combustion
Livret Bac : Thème 1 bis
2. Mouvement et interactions
Ch. 11
Modélisation d'interactions fondamentales
Ch. 12
Description d'un fluide au repos
Ch. 13
Mouvement d'un système
Livret Bac : Thème 2
3. L'énergie, conversions et transferts
Ch. 14
Études énergétiques en électricité
Ch. 15
Études énergétiques en mécanique
Livret Bac : Thème 3
4. Ondes et signaux
Ch. 16
Ondes mécaniques
Ch. 17
Images et couleurs
Ch. 18
Modèles ondulatoire et particulaire de la lumière
Livret Bac : Thème 4
Méthode
Fiches méthode
Fiche méthode compétences
Annexes
Chapitre 12
Exercices
Pour s'entraîner
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20 Sphère de Magdebourg
✔ RAI/MOD : Faire le bilan des forces✔ REA : Effectuer des calculs littéraux et numériques

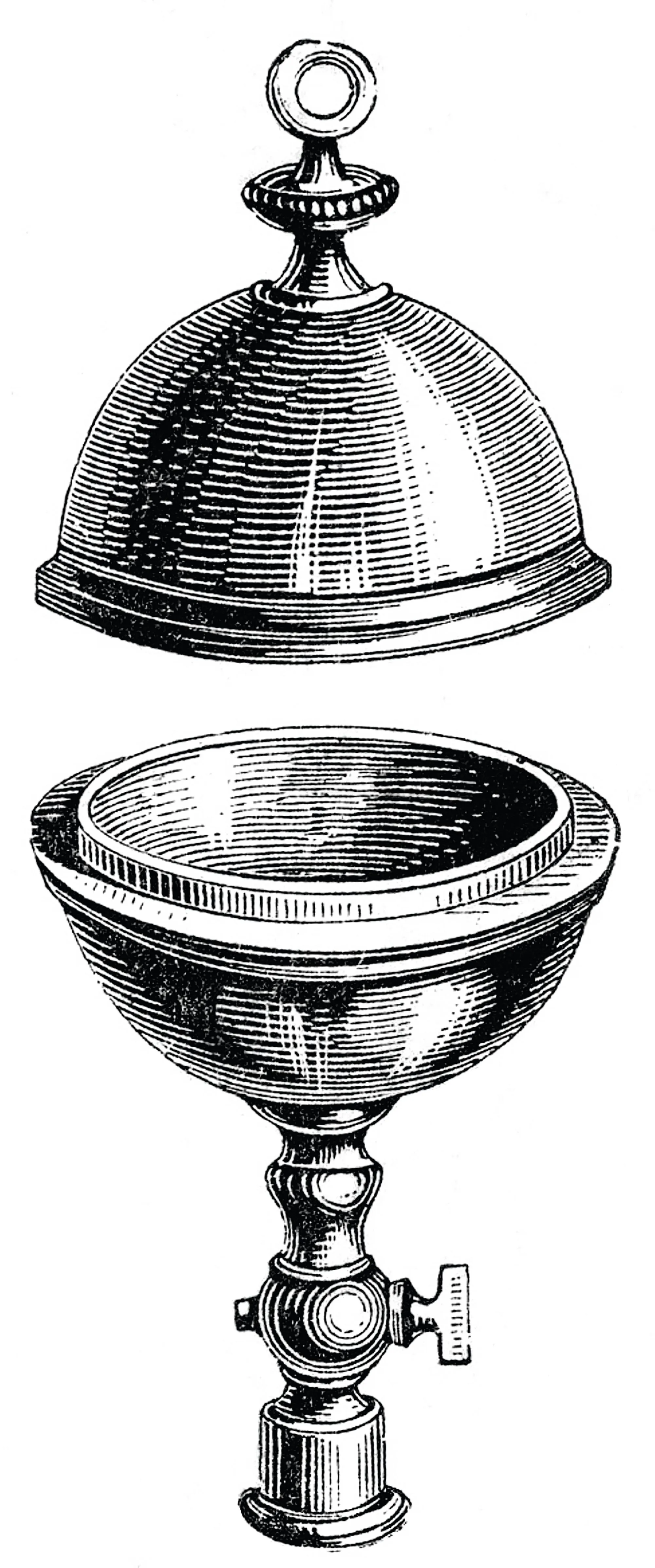
Les sphères de Magdebourg sont deux hémisphères s'emboîtant l'un dans l'autre, et dans lesquelles on peut faire le vide.
1. Pourquoi est-il très difficile, une fois le vide fait, de séparer les hémisphères ?
2.
Calculer la force qu'il faudrait appliquer pour séparer deux hémisphères de rayon R.
Données
- Rayon de la sphère originale : R= 28 cm.
- La force pressante sur un hémisphère est égale à la force pressante s'appliquant sur un disque de même rayon.
Histoire des sciences
À partir de 1654, le bourgmestre de Magdebourg, Otto von Guericke (1602-1686), réalise de nombreuses
démonstrations à l'aide de divers hémisphères dans lesquels il fait le vide. Trente chevaux n'arrivent pas à
les séparer ! Ces démonstrations ont un grand succès et sont reproduites dans de nombreux endroits.
Elles jouent un rôle important dans la confirmation de l'existence du vide et l'explication de la pression
atmosphérique.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21 La statique des fluides spatiaux en QCM
✔ APP : Formuler le résultat attendu
Sur la Lune (g_{\text{Lune}}= 1,62 N·kg-1), à l'intérieur d'une station remplie d'air terrestre, se trouve un réservoir d'eau de 3 mètres de haut. Une vanne de vidange se trouve au fond du réservoir. Comparer cette situation avec ce qu'il se passerait sur Terre.
1. Le poids de l'eau serait :
1. Le poids de l'eau serait :
2. La pression de l'eau au fond du réservoir :
3. Dans une zone de l'espace où l'intensité de pesanteur est supposée nulle :
3. Dans une zone de l'espace où l'intensité de pesanteur est supposée nulle :
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22 Convertir les degrés Celsius en kelvin
✔ REA : Effectuer des calculs littéraux et numériques
La température en kelvin (K) est notée T et celle en degré Celsius (°C) est notée \theta. On note également qu'une variation de température a la même valeur dans les deux systèmes d'unités : \Delta T=\Delta \theta.
1. Exprimer la relation mathématique permettant de calculer une température en kelvin à partir d'une température en degré Celsius connue.
2. Exprimer la relation mathématique permettant de calculer une température en degré Celsius à partir d'une température en kelvin connue.
La température en kelvin (K) est notée T et celle en degré Celsius (°C) est notée \theta. On note également qu'une variation de température a la même valeur dans les deux systèmes d'unités : \Delta T=\Delta \theta.
1. Exprimer la relation mathématique permettant de calculer une température en kelvin à partir d'une température en degré Celsius connue.
2. Exprimer la relation mathématique permettant de calculer une température en degré Celsius à partir d'une température en kelvin connue.
3.
À l'aide des expressions précédentes, compléter le tableau de température suivant.
| Température... | T(K) | \theta(°C) |
| du laboratoire | | 25 |
| d'ébullition de l'azote | 77,36 | |
| de surface du Soleil | 5 750 | |
| de fusion du cyclohexane | | 6,5 |
| du zéro absolu | 0 | |
| de la glace fondante | | 0 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Comprendre les attendusProblème d'eau courante
✔ REA : Effectuer des calculs littéraux
Voici le schéma d'un château d'eau (réserve d'eau) relié à un immeuble par un tuyau.
Déterminer la hauteur h_{2} jusqu'à laquelle l'eau peut monter.
Détails du barème
TOTAL /6,5 pts
1 pt
Positionner deux points A et B situés sur les deux surfaces libres du fluide.2 pts
Vérifier que les pressions du fluide P_{1} et P_{2} soient égales à la pression atmosphérique.1 pt
Écrire la relation fondamentale de la statique des fluides avec les bonnes notations.2 pts
En raisonnant sur les pressions, trouver le lien entre h_{1} et h_{2}.0,5 pt
Conclure sur la question posée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24Respirer au sommet
✔ VAL : Rechercher les sources d'erreur

Le Mont-Blanc est le plus haut sommet d'Europe, culminant à 4 810 m d'altitude. À son sommet la pression atmosphérique moyenne mesurée n'est plus que de 554,6 hPa, ce qui rend la respiration plus difficile.
1.
À l'aide de la relation fondamentale de la statique des fluides, calculer la pression P_{\text{sommet}} au sommet du Mont-Blanc.
2. Ce résultat correspond-il aux mesures ? Faire la liste des raisons qui peuvent expliquer cela.
2. Ce résultat correspond-il aux mesures ? Faire la liste des raisons qui peuvent expliquer cela.
Données
- Masse volumique de l'air à pression atmosphérique : \rhoair = 1,22 kg·m-3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25 Attention à la remontée !
✔ REA : Effectuer des calculs littéraux et numériques

Les plongeurs utilisent de plus en plus des bouteilles de nitrox, il s'agit d'un mélange de dioxygène et de diazote. Il est stocké sous pression dans une bouteille et respiré à la pression de l'eau autour du plongeur.
1.
Pourquoi est-il nécessaire que la pression du nitrox respiré soit la même que la pression de l'eau ?
2. Calculer le volume V_{2} qu'occuperait à la surface le gaz inspiré à 5 m de profondeur.
3. Si le plongeur retenait sa respiration lors des 5 derniers mètres de la remontée, quel risque prendrait-il ?
2. Calculer le volume V_{2} qu'occuperait à la surface le gaz inspiré à 5 m de profondeur.
3. Si le plongeur retenait sa respiration lors des 5 derniers mètres de la remontée, quel risque prendrait-il ?
Données
- Volume de gaz dans les poumons : V_{1}= 5,0 L ;
- Pression de l'eau à 5 m de profondeur : P(5 m) = 1,5 bar.
Information
Les paliers de décompression que doivent respecter les plongeurs ne sont pas dus seulement à la pression du gaz dans les poumons. Le diazote respiré se dissout partiellement dans le sang et risque, en cas de remontée trop rapide, de former des bulles dans les vaisseaux sanguins bloquant la circulation du sang.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Piston sous pression
✔ REA : Effectuer des calculs littéraux et numériques
On pose une masse sur un piston contenant de l'air à la pression atmosphérique. L'air contenu dans le piston va se comprimer jusqu'à un point d'équilibre.
1.
Faire le bilan des forces s'appliquant sur le piston.
2. Calculer le coefficient de compression \gamma=\dfrac{V_{1}}{V_{0}}.
3. Que se passe-t-il au niveau microscopique dans le piston ?
2. Calculer le coefficient de compression \gamma=\dfrac{V_{1}}{V_{0}}.
3. Que se passe-t-il au niveau microscopique dans le piston ?
Données
- Volume du piston : V_0= 200 cm3 ;
- Surface du piston : S= 20 cm2 ;
- Masse : m= 500 g.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Copie d'élève à commenter
Proposer une justification pour chaque erreur relevée par le correcteur.Énoncé : Un humain peut continuer à inspirer de l'air à pression atmosphérique (P_{0}= 1 013 hPa) si la surpression subie sur sa cage thoracique ne dépasse pas 11 000 Pa. Peut-on respirer sous l'eau avec un tuba de 2,0 m de long ? On rajoute 20 cm à cette longueur pour tenir compte de la distance bouche-poumons.
À deux mètres de profondeur, la pression de l'eau sur la cage thoracique sera plus grande qu'à la surface, en raison du principe fondamental de l'hydrostatique :
P=P_{0}+\rho \cdot g \cdot h.
Avec : g= 9,81 N·kg-1 ; \rhoeau = 1 000 kg·m-3 ; h= 2 m + 0,2 m ; P_{0}= = 1 013 hPa.
D'où :
P=1 013 Pa + 1 000 kg·m-3 \times 9,81 N·kg-1 \times 2,02 m = 22 600 Pa.
À unepression supérieure à 11 000 Pa on ne peut
pas expirer et la respiration devient impossible. P-P_0 étant supérieure à 11 000 Pa, on ne pourra pas respirer avec un tuba de deux mètres de long.
P=P_{0}+\rho \cdot g \cdot h.
Avec : g= 9,81 N·kg-1 ; \rhoeau = 1 000 kg·m-3 ; h= 2 m + 0,2 m ; P_{0}= = 1 013 hPa.
D'où :
P=
À une
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28Deux récipients remplis
✔ RAI/ANA : Utiliser des documents pour répondre à une
problématiqueDeux récipients sont partiellement remplis par un liquide et reliés par un tuyau.

l'aide du principe fondamental de l'hydrostatique, expliquer pourquoi la surface libre du liquide reste au même niveau dans les deux récipients même lorsqu'ils ne sont pas à la même hauteur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29L'air au sommet de l'Everest
✔ RAI/ANA : Faire le lien entre les modèles microscopiques et
grandeurs macroscopiques
Au sommet de l'Everest la pression atmosphérique est si basse (31 460 Pa) que la respiration est très difficile et qu'il n'est pas possible de survivre plus de quelques jours. On peut raisonner en considérant qu'une personne ne reçoit au sommet que 30 % de l'oxygène qu'elle reçoit au niveau de la mer.
1. Au sommet de l'Everest, quel volume occuperait une quantité d'air dont le volume serait d'un litre au niveau de la mer ?
1. Au sommet de l'Everest, quel volume occuperait une quantité d'air dont le volume serait d'un litre au niveau de la mer ?
2.
Représenter deux volumes identiques, l'un contenant de l'air pris au niveau du sol et l'autre au niveau du sommet de l'Everest. Faire apparaître les différences au niveau microscopique.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30 Le tonneau de Pascal
✔ REA : Effectuer des calculs littéraux et numériquesHistoire des sciences
Cette expérience, appelée « crève-tonneau », a été menée pour la première fois par Blaise Pascal (1623-1662) en 1646. Elle est représentée sur l'image ci-dessus. C'est Pascal qui a également exprimé le principe fondamental de l'hydrostatique. Il a donné son nom à l'unité de pression du système international d'unités (Pa).

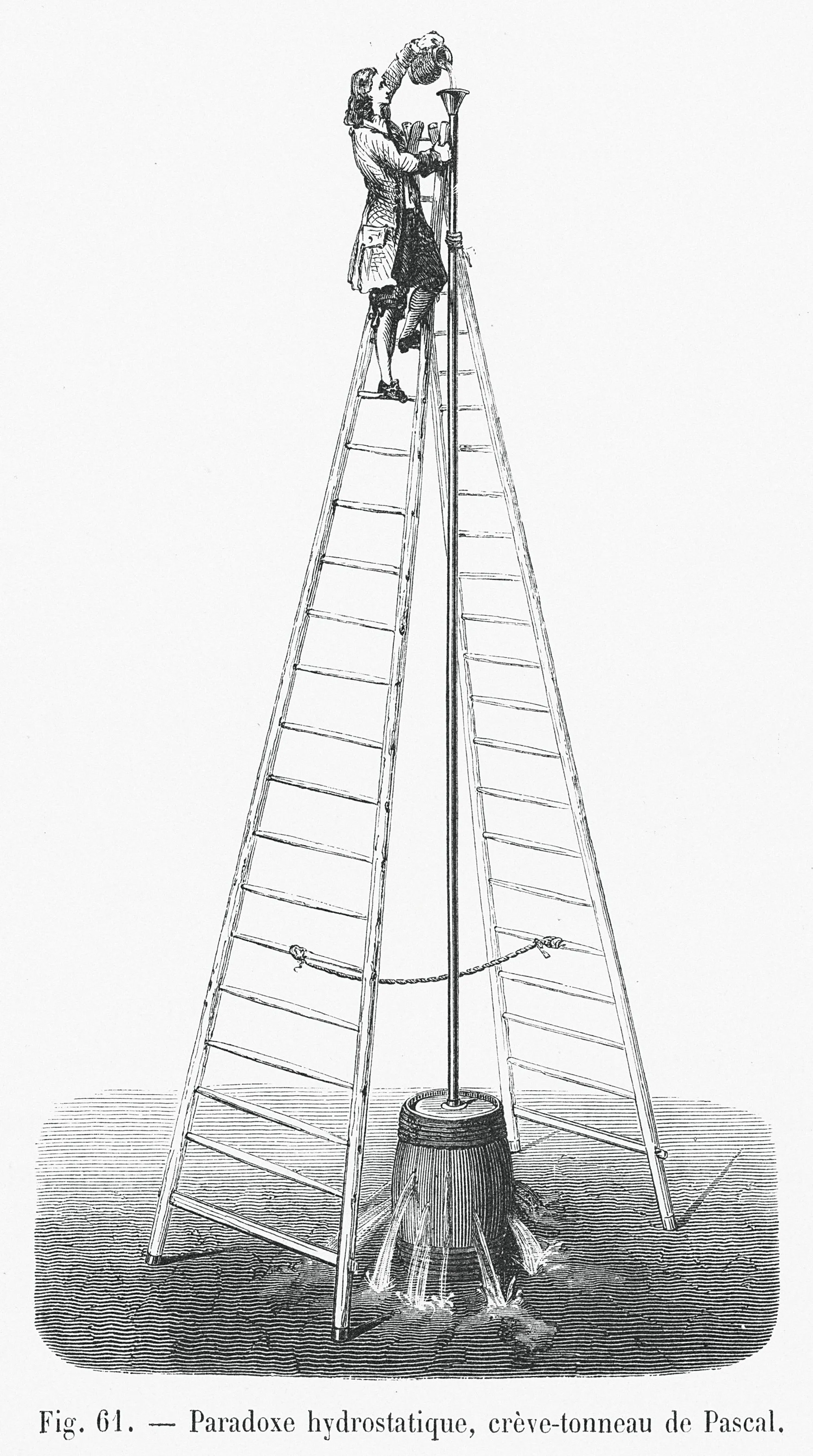
Soit un tonneau entièrement rempli d'eau. On y insère un tube de dix mètres de haut, que l'on remplit d'eau. Le tonneau se met à fuir, puis casse.
1. À quelle pression est soumis le tonneau une fois le tube rempli ?
2. Pourquoi le tonneau a-t-il cédé ?
3. Quel doit être le diamètre du tube pour qu'un litre d'eau suffise à le remplir ? Dans ce cas, le tonneau cède-t-il ?
1. À quelle pression est soumis le tonneau une fois le tube rempli ?
2. Pourquoi le tonneau a-t-il cédé ?
3. Quel doit être le diamètre du tube pour qu'un litre d'eau suffise à le remplir ? Dans ce cas, le tonneau cède-t-il ?
Données
- Surpression maximale supportable par le tonneau : \Delta P= 5 \times 104 Pa.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31 Deux récipients remplis
✔ REA : Effectuer des calculs littéraux et numériques
Une voiture se trouve sur un pont élévateur (voir p. 247), mais cette fois à une hauteur h_{1} au-dessus du sol.
1. Choisir deux points pertinents et écrire la relation fondamentale de la statique entre ces deux points.
2.
Faire le bilan des forces s'appliquant sur le pont élévateur.
3. Calculer la pression P_{\text{air}} fournie par le compresseur pour maintenir la voiture à cette hauteur.
3. Calculer la pression P_{\text{air}} fournie par le compresseur pour maintenir la voiture à cette hauteur.
Données
- m_\text{{voiture}}= 2,1 \times 103 kg ;
- h_{1}= 1,80 m ;
- S_{1}= 5,0 cm2 ;
- S_{2}= 1,2 m2 ;
- Le fluide utilisé est une huile hydraulique : \rho_{\text{huile}} = 883 kg·m‑3 ;
- On considère la masse du piston et du pont élévateur comme négligeable.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
ASous‑marin
✔ REA : Effectuer des calculs littéraux et numériques
Les hublots d'un sous‑marin sont de forme circulaire, de rayon r=20 cm. Ils restent étanches tant que la force pressante exercée par l'eau sur le hublot ne dépasse pas F_{\max }=1{,}16 \times 10^{6} N. On considère que la pression en surface est P_{0}=1{,}013 bar.
Pesanteur terrestre : g=9{,}81 N·kg-1.
Les hublots d'un sous‑marin sont de forme circulaire, de rayon r=20 cm. Ils restent étanches tant que la force pressante exercée par l'eau sur le hublot ne dépasse pas F_{\max }=1{,}16 \times 10^{6} N. On considère que la pression en surface est P_{0}=1{,}013 bar.
- Calculer la profondeur maximale que peut atteindre ce sous‑marin tout en restant étanche.
Données
Masse volumique de l'eau de mer : \rho_{\text {eau }}=1{,}03 \times 10^{3} kg·m-3.Pesanteur terrestre : g=9{,}81 N·kg-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
CLa loi des gaz parfaits
✔ MATH : Calcul littéral
Lorsque la pression n'est pas trop importante, les gaz peuvent être modélisés par un modèle simple appelé modèle du gaz parfait. Dans ce modèle, la pression P en Pa, la température T en K, le volume V en m3 et la quantité de matière n du gaz en mol sont reliés par la formule : P⋅V=R⋅n⋅T, où R est la constante des gaz parfait et vaut 8{,}314 Pa·m3·mol-1·K-1.
1. Montrer que la Loi de Boyle‑Mariotte est une conséquence de la loi des gaz parfaits. Pourquoi n'est‑elle valable qu'à température constante ?
2. Montrer que le volume molaire d'un gaz parfait est de 24{,}0 L·mol-1 à température et pression standards (P_{\text {standard }}=1\:013 hPa et T_{\text {standard }}=20^{\circ} \mathrm{C}).
3. Exprimer la masse volumique d'un gaz parfait en fonction de la pression P, la température T et sa masse molaire M.
Lorsque la pression n'est pas trop importante, les gaz peuvent être modélisés par un modèle simple appelé modèle du gaz parfait. Dans ce modèle, la pression P en Pa, la température T en K, le volume V en m3 et la quantité de matière n du gaz en mol sont reliés par la formule : P⋅V=R⋅n⋅T, où R est la constante des gaz parfait et vaut 8{,}314 Pa·m3·mol-1·K-1.
1. Montrer que la Loi de Boyle‑Mariotte est une conséquence de la loi des gaz parfaits. Pourquoi n'est‑elle valable qu'à température constante ?
2. Montrer que le volume molaire d'un gaz parfait est de 24{,}0 L·mol-1 à température et pression standards (P_{\text {standard }}=1\:013 hPa et T_{\text {standard }}=20^{\circ} \mathrm{C}).
3. Exprimer la masse volumique d'un gaz parfait en fonction de la pression P, la température T et sa masse molaire M.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
BBallon‑sonde et poussée d'Archimède
✔ REA : Effectuer des calculs littéraux et numériques
On considère un ballon‑sonde de volume au décollage V_{0}=33 m3, contenant une masse m_{\mathrm{He}}=5{,}5 kg d'hélium gazeux. La masse de la nacelle et des instruments est m_{\mathrm{nac}}=2{,}5 kg. On considère qu'au décollage, la pression est P_{0}=1{,}0 bar et la température T _{0}=17^{\circ} \mathrm{C}.
1. Décollage
a. Calculer le poids P_{b} du ballon et de sa nacelle (hélium compris).
b. Calculer la valeur de la poussée d'Archimède F_{A} s'exerçant sur le ballon. Est‑elle suffisante pour vaincre la gravité et faire décoller le ballon ?
2. Loi de Boyle‑Mariotte
a. Calculer le volume V' du ballon lorsque la pression est P^{\prime}=0,4 bar.
b. Lorsque le volume du ballon atteint V_{\max }=2{,}1 \times 10^{3} m3, le ballon éclate. Quelle est alors la valeur \mathrm{P}_{\min } de la pression ?
Pesanteur terrestre : g =9{,}81 N·kg-1
Masse volumique de l'air à 0 m d'altitude : \rho_{\text {air }}=1{,}22 kg·m-3
On considère un ballon‑sonde de volume au décollage V_{0}=33 m3, contenant une masse m_{\mathrm{He}}=5{,}5 kg d'hélium gazeux. La masse de la nacelle et des instruments est m_{\mathrm{nac}}=2{,}5 kg. On considère qu'au décollage, la pression est P_{0}=1{,}0 bar et la température T _{0}=17^{\circ} \mathrm{C}.
Doc. 1
Poussée d'Archimède
La poussée d'Archimède est une force qui s'exerce sur tout corps plongé dans un fluide (ie un gaz ou un liquide). Cette force est verticale vers le haut, de valeur égale au poids d'un volume de fluide identique à celui de l'objet.
1. Décollage
a. Calculer le poids P_{b} du ballon et de sa nacelle (hélium compris).
b. Calculer la valeur de la poussée d'Archimède F_{A} s'exerçant sur le ballon. Est‑elle suffisante pour vaincre la gravité et faire décoller le ballon ?
2. Loi de Boyle‑Mariotte
a. Calculer le volume V' du ballon lorsque la pression est P^{\prime}=0,4 bar.
b. Lorsque le volume du ballon atteint V_{\max }=2{,}1 \times 10^{3} m3, le ballon éclate. Quelle est alors la valeur \mathrm{P}_{\min } de la pression ?
Données
Pesanteur terrestre : g =9{,}81 N·kg-1
Masse volumique de l'air à 0 m d'altitude : \rho_{\text {air }}=1{,}22 kg·m-3
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
