Mathématiques 4e - 2022
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algorithmique et programmation
Dossier Scratch
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d'équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Prolongement
Chapitre 13
Activités
Découvrir le chapitre : géométrie plane
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
La géométrie de la règle et du compas
L'ensemble des résultats que l'on trouve dans Les Éléments, l'encyclopédie mathématique rédigée
par Euclide (environ 300 av. J.-C.), se basent principalement sur des raisonnements géométriques
(y compris en algèbre et en arithmétique) et reposent sur des définitions, des postulats (principes
qui permettent de construire la géométrie d'Euclide), des axiomes, des théorèmes et des exemples
de constructions. Les Eléments constituent ainsi le premier modèle d'une science déductive.
Le livre I énonce les propriétés de base de la géométrie plane : les définitions des principaux
objets géométriques (point, droite, polyèdre, cercle, etc.), les principes d'orthogonalité et de
parallélisme, les égalités angulaires et les cas d'égalité des triangles (étudiés dans ce chapitre).
Fondamentalement, ces définitions ancrent la géométrie euclidienne dans un système de
constructions théoriques qui n'utilisent que la règle et le compas.
En cherchant à rendre les constructions géométriques plus faciles et en même temps plus précises, le mathématicien Lorenzo Mascheroni publie un ouvrage remarquable en 1797, Géométrie du compas. Il y démontre un théorème qui porte son nom : toute construction ou problème pouvant se résoudre à la règle et au compas peut se résoudre uniquement au compas.
En cherchant à rendre les constructions géométriques plus faciles et en même temps plus précises, le mathématicien Lorenzo Mascheroni publie un ouvrage remarquable en 1797, Géométrie du compas. Il y démontre un théorème qui porte son nom : toute construction ou problème pouvant se résoudre à la règle et au compas peut se résoudre uniquement au compas.


Tracer un carré en utilisant uniquement un compas et une règle
non graduée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Des égalités de figures géométriques
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Partie 1 : Définition des triangles égaux.
1
Compléter le tableau suivant en mesurant les angles des triangles présents sur cette
.| Triangles | Mesures d'angles |
|---|---|
| 1 | 100°, 28° et |
| 2 | |
Coup de pouce
Pour mesurer
précisément les angles, vous pouvez
prolonger les côtés des triangles.
2
Que peut-on dire de ces triangles ?
3
Découper ces triangles. Semblent-ils tous superposables ?
4
Mesurer les longueurs des côtés des triangles superposables deux à deux. Que remarque-t-on ?5
On dit que les triangles 2 et 3 sont égaux, ainsi que les triangles 1 et 4.
Donner une définition possible pour deux triangles égaux.
Partie 2 : Propriétés des triangles égaux.
1
a. Tracer un triangle \text{ABC} tel que \mathrm{AB}=4 \mathrm{~cm} et \mathrm{AC}=2 \mathrm{~cm}.
b. Les triangles obtenus dans la classe sont-ils tous égaux entre eux ?
2
a. Tracer un triangle \text{DEF} tel que \widehat{\mathrm{EDF}}=52^{\circ} et \widehat{\mathrm{EFD}}=28^{\circ}.
b. Les triangles obtenus dans la classe sont-ils tous égaux entre eux ?
Bilan
Quelles semblent être les conditions nécessaires et suffisantes pour que deux triangles soient égaux ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Une nouvelle transformation
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
M. Pi, professeur de mathématiques, demande à ses élèves d'utiliser différentes transformations du plan sur GeoGebra pour obtenir les images du triangle rouge. Voici une capture d'écran du travail d'Emma.

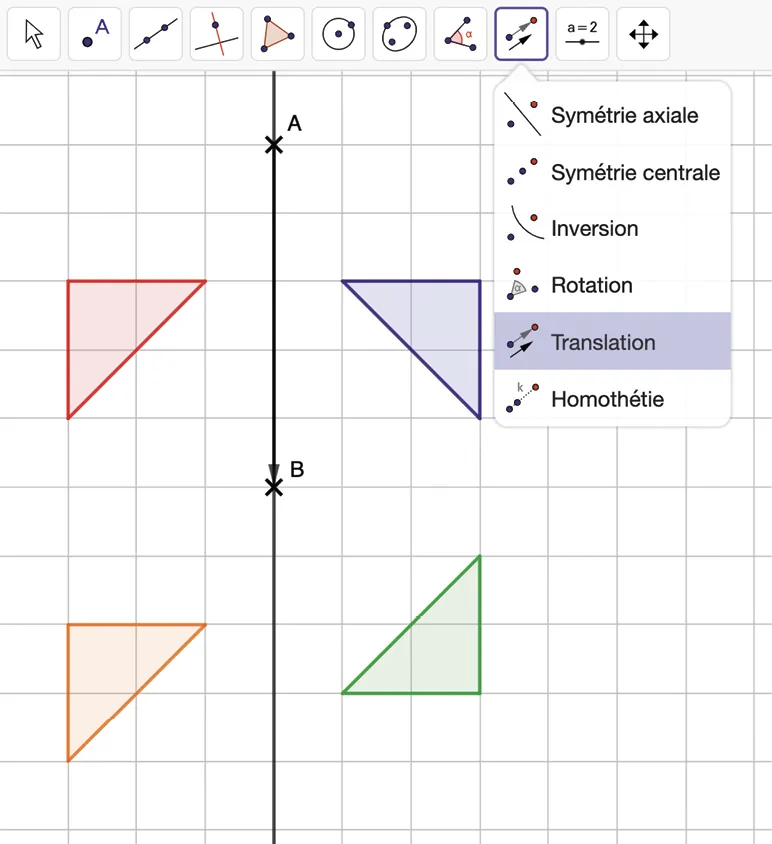
1
a. Quelle transformation a-t-elle utilisée pour
obtenir le triangle bleu à partir du rouge ?
b. Pour l'obtenir, quels points a-t-elle utilisés ?
2
a. Quelle transformation a-t-elle utilisée pour
obtenir le triangle vert à partir du rouge ?
b. Pour l'obtenir, quel point a-t-elle utilisé ?
3
En appuyant sur le point \text{A} puis le point \text{B}, une flèche s'est automatiquement créée. Elle
schématise la translation qui permet de passer du triangle rouge au triangle orange. En utilisant
les caractéristiques de cette flèche, décrire cette nouvelle transformation.
Coup de pouce
La longueur, le sens, la direction sont des
caractéristiques qui peuvent être utilisées pour décrire une translation.
4
Les triangles rouge et orange sont-ils égaux ? Justifier.
Bilan
Lorsqu'on obtient l'image d'une figure par une translation, des grandeurs sont conservées. Lesquelles ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
