Synthèse

Romain et Arnaud jouent l'un contre l'autre à une manche du jeu du Béret. Dans ce jeu, les joueurs de chaque camp doivent être positionnés à la même distance du béret, l'objectif étant d'attraper le béret et de le ramener dans son camp le plus rapidement possible.
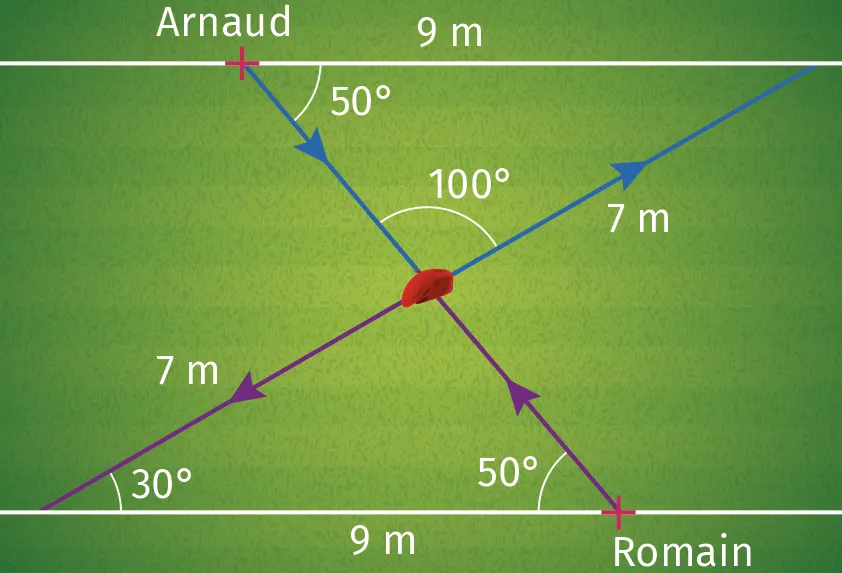
Arnaud remporte le point dans son duel contre Romain, mais Romain n'est pas d'accord et pense que le béret n'était pas positionné correctement.
En utilisant les informations du schéma suivant et en justifiant la réponse, dire si Romain a raison ou tort.

1. Les triangles suivants sont-ils égaux pour $x=2$ ? Justifier.

2. Pour quelle valeur de $x$ ces triangles sont-ils égaux ? Justifier.

D'après Brevet, Polynésie, septembre 2020
On considère le motif initial suivant. Il est composé d'un carré ABCE de côté 5 cm et d'un triangle EDC, rectangle et isocèle en D.

On réalise un pavage du plan en partant du motif initial et en utilisant différentes transformations du plan.

Le polygone $\text{FGHIJ}$ est l'image de $\text{ABCDE}$, composé d'un carré $\text{ABCE}$ et d'un triangle $\text{CDE}$, par la translation qui transforme $\text{A}$ en $\text{F}$.

1. Quelle est la longueur de $[\mathrm{GH}]$ ? Justifier.

2. Que peut-on dire des droites $(\mathrm{FJ})$ et $(\mathrm{GH})$ ?

3. a. Quelle est la mesure de $\widehat{\mathrm{ECD}}$ ?

b. En déduire la mesure de l'angle $\widehat{\mathrm{JHI}}$.

Juliette et Benoit ont fait un footing au parc de la Tête d'Or à Lyon mais ils n'ont pas couru ensemble. Voici les parcours qu'ils ont réalisés.

1. Juliette soutient à Benoit qu'ils ont couru la même distance. A-t-elle raison ?

2. La longueur manquante du triangle rouge est 385 m. Quelle distance totale, en kilomètre, Benoit a-t-il parcouru sachant qu'il a réalisé trois fois le même tour ?

Jack Sparrow et Barbossa, représentés respectivement sur la carte par les points $\text{J}$ et $\text{B}$, se disputent le trésor de l'Île des pirates (noté $\text{T}$).

Jack Sparrow effectue des translations qui transforment $\text{C}$ en $\text{E}$, puis $\text{S}$ en $\text{E}$, ensuite $\text{N}$ en $\text{S}$, et enfin $\text{O}$ en $\text{E}$.
Barbossa effectue les déplacements suivants.


Lequel des deux pirates va parcourir la plus courte distance pour atteindre le trésor ?