Enseignement scientifique 1re - 2023

Retourner à l'accueil
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Esprit critique
Une longue histoire de la matière
Une longue histoire de la matière
Ouverture de thème p. 18-20
Ch. 1
Les éléments chimiques
Ch. 2
Les cristaux, des édifices ordonnés
Ch. 3
Une structure complexe : la cellule
Se préparer à l'évaluation
Exercicesp. 71-73
Le Soleil, notre source d'énergie
Le Soleil, notre source d’énergie
Ouverture de thème p. 74-76
Ch. 4
Le rayonnement solaire
Ch. 5
Le bilan radiatif terrestre
Ch. 6
Énergie solaire, photosynthèse et nutrition
Ch. 7
Énergie solaire et humanité
Se préparer à l'évaluation
Exercicesp. 141-143
La Terre, un astre singulier
La Terre, un astre singulier
Ouverture de thème p. 144-146
Ch. 8
La forme de la Terre
Ch. 9
L’Histoire de l'âge de la Terre
Ch. 10
La Terre dans l'Univers
Se préparer à l'évaluation
Exercicesp. 193-195
Son et musique, porteurs d'information
Son et musique, porteurs d’information
Ouverture de thème p. 196-198
Ch. 11
Son et musique
Ch. 12
Le son, une information à coder
Ch. 13
Entendre et protéger son audition
Se préparer à l'évaluation
Exercicesp. 243-244
Projet expérimental et numérique
Livret Maths
Résolution d’équation
Livret mathsp. 263
Calcul algébrique
Livret mathsp. 264-265
Puissances, écriture scientifique et ordre de grandeur
Livret mathsp. 266-267
Suites géométriques à termes strictement positifs, décroissance exponentielle
Livret mathsp. 268
Grandeurs et mesures, grandeurs dérivées
Livret mathsp. 269
Proportionnalités, proportions, pourcentages, échelle
Livret mathsp. 270-271
Statistiques
Livret mathsp. 272-273
Lecture et représentation graphique
Livret mathsp. 274-275
Fonctions trigonométriques
Livret mathsp. 276
Géométrie
Livret mathsp. 277-279
Théorème de Pythagore
Livret mathsp. 280
Représentation dans l'espace, perspective cavalière
Livret mathsp. 281
Annexes
Livret maths 10

Géométrie

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours A
Géométrie du disque

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Périmètre et aire

  • Pour calculer le périmètre P d'un cercle de rayon r, on utilise la formule : P=2 \pi \cdot r
  • Pour calculer l'aire A d'un disque de rayon r, on utilise la formule: A=\pi \cdot r^{2}

Disque
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Longueur d'un arc de cercle

  • La longueur de l'arc \ell entre deux points \mathrm{A} et \mathrm{B} est proportionnelle à l'angle \alpha qu'il intercepte.

  • On utilise ce tableau de proportionnalité, où r et \alpha sont connus, et \ell est à calculer.
    • Longueur de l'arcP=2 \pi \cdot r\ell
    Angle (\mathrm{rad})2 \pi\alpha

  • On a donc la formule suivante où \alpha doit être exprimée en radian (rad) : \ell=\alpha \cdot r

Disque
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Aire d'un secteur circulaire

  • L'aire A_{\mathrm{AOB}} est proportionnelle à l'angle \alpha qu'il intercepte.

  • On utilise ce tableau de proportionnalité, où r et \alpha sont connus, et A_{\text {АОв }} est à calculer.
    • Aire du secteurA=\pi \cdot r^2A_{\mathrm{AOB}}
    Angle (rad)2 \pi\alpha

  • On a donc la formule suivante où \alpha doit être exprimée en radian (rad) : A_{\mathrm{AOB}}=\frac{\alpha \cdot r^{2}}{2}
    • Remarque
    Pour rappel, la conversion pour exprimer un angle en degré (°) vers sa valeur en radian (rad) est proportionnelle: 2 \pi rad = 360°.

Disque
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 1

Calculez :

a. le périmètre d'un cercle de rayon 15 cm ;
b. le périmètre d'un cercle de diamètre 25 dam ;
c. l'aire d'un disque de rayon 75 mm ;
d. l'aire d'un disque de diamètre 170 nm.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 2
Déterminez le rayon d'un cercle :

a. de périmètre 6 500 km
b. d'aire 494 000 m2
Arrondissez les résultats à 10-3 près.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 4
Déterminez la longueur de l'arc \ell, dans la figure suivante.

Disque
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 5
La nouvelle définition du parsec datant de 2015 correspond au « rayon d'un cercle dont l'arc, soutenu par un angle au centre d'une seconde d'arc (1ˮ), mesure exactement une unité astronomique ».

Disque


Calculez la valeur d'un parsec en kilomètre (km). Écrivez le résultat en notation scientifique, puis en année-lumière (al).
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 6
Les cercles de centres \mathrm{A} et \mathrm{B} ont pour rayon 10 cm. Le triangle \mathrm{ABC} est équilatéral. \mathrm{C} et \mathrm{D} sont symétriques par rapport à la droite \mathrm{AB}. Calculez le périmètre et l'aire de la partie jaune.

Disque
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours B
Géométrie de la sphère

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Propriété

  • La sphère de centre \mathrm{O} et de rayon r est formée de tous les points \mathrm{M} de l'espace tels que \mathrm{OM}=r.
  • La boule de centre \mathrm{O} et de rayon r est formée de tous les points \mathrm{M} de l'espace tels que \mathrm{OM} \leqslant r.
  • Le volume de la boule de rayon r est donné par la formule : V=\frac{4}{3} \pi \cdot r^3.
  • L'aire de la sphère de rayon r est donnée par la formule : A=4 \pi \cdot r^2.
  • Un grand cercle est un cercle de centre \mathrm{O} et de rayon r. Son périmètre définit la circonférence de la sphère.
Disque
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 1

Calculez l'aire d'une sphère et le volume de la boule associée lorsque celle-ci a :

a. un rayon 30 cm.
b. un diamètre 5,5 cm.
c. un grand cercle ayant un périmètre d'un mètre.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 2

Déterminez le rayon d'une boule contenant 1 000 L.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 3

On assimile la Terre à une sphère de rayon 6 370 km. La croûte terrestre a une épaisseur moyenne d'environ 40 km.

Calculez le volume de la Terre et de la croûte terrestre. Quelle proportion de la planète représente-t-elle ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 4

On considère une sphère de rayon 10 cm et \mathrm{H} un point à l'intérieur de la boule à 7 cm du centre.

Calculez le rayon et l'aire du disque de centre \mathrm{H}, intersection de la sphère avec le plan parallèle à l'équateur et passant par \mathrm{H}.

Disque
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 5

a. Décrivez l'évolution de l'aire et du volume d'une sphère lorsqu'on double son rayon.
b. Y a-t-il proportionnalité entre le rayon d'une sphère et son aire ? Qu'en est-il de son volume ?
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 6

Sur l'équateur, deux lieux sont séparés de 800 km. Sachant que le rayon de la Terre vaut 6 370 km, déterminez l'angle interceptant cette distance.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 7

En coupant une sphère par un plan à une distance h du pôle, on construit une calotte sphérique. Son aire et son volume s'expriment selon :

  • A=2 \pi \cdot r \cdot h
  • V=\pi h^2\left(r-\frac{h}{3}\right)

Calculez l'aire et le volume d'une calotte sphérique terrestre coupée à 100 km du pôle sachant que le rayon de la Terre vaut 6 370 km.
Disque
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours C
Repérage sur la Terre

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Pour retrouver les notions liées au repérage sur la Terre, rendez-vous aux
pages 154 et 155
.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Données

Rayon de la Terre : \mathrm{R}_{\mathrm{T}}=6370 km
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 1
Quito (Équateur) et Kisangani (République démocratique du Congo) sont deux villes sur l'équateur de longitudes 78°30' O et 25°12' E.

a. Déterminez l'angle formé entre ces deux villes avec le centre de la Terre.
b. Calculez la distance qui les sépare à la surface du globe.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 2
Hanoï (Vietnam) et Jakarta (Indonésie), sont à la même longitude (106°E) et ont pour latitude 21°N et 6°S.

a. Déterminez l'angle formé entre ces deux villes avec le centre de la Terre.
b. Calculez la distance qui les sépare à la surface du globe.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
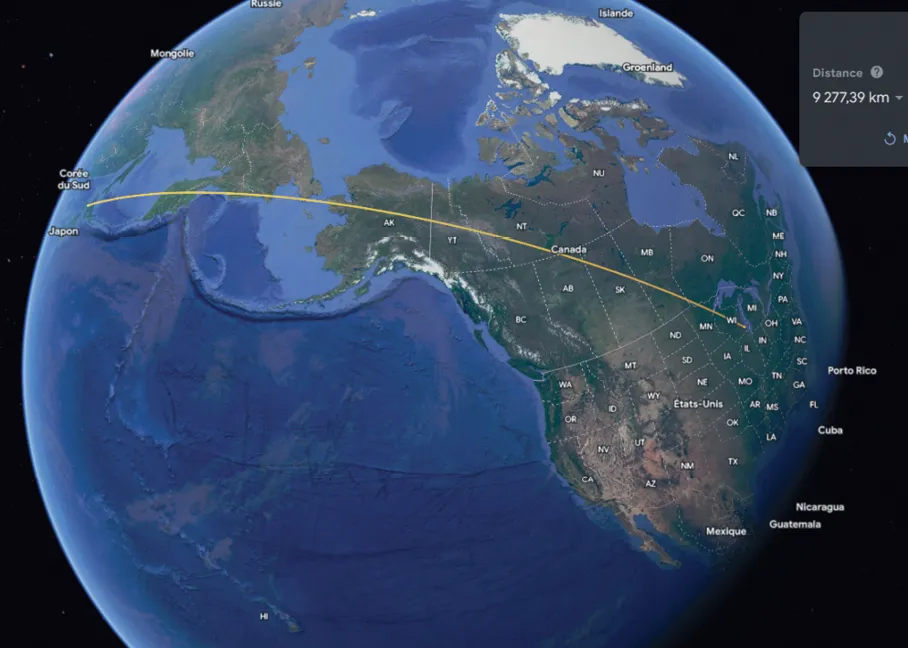
Exercice 3
Milwaukee (Wisconsin, États-Unis) et Sapporo (Japon) sont deux villes à la latitude de 43°N, distantes de 9 300 km environ. Sachant que Sapporo est à la longitude 141°E, calculez la longitude de Milwaukee.

Placeholder pour Image de la terre d'un trajet entre Milwaukee (Wisconsin, États-Unis) et Sapporo (Japon)Image de la terre d'un trajet entre Milwaukee (Wisconsin, États-Unis) et Sapporo (Japon)
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 4
Déterminez la distance qui sépare deux points antipodaux (diamétralement opposés à la surface de la Terre).

Remarque
Le point aux antipodes de la France est situé près de la Nouvelle-Zélande.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 5
Milan (Italie) et Montréal (Canada) sont à la même latitude (45°3 N environ), et distantes de 6 020 km. Calculez l'écart entre leurs longitudes.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Point de cours D
Rotation

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Définition

Une sphère est en rotation si la trajectoire de tous les points à sa surface sont des cercles dont les centres \mathrm{O} se situent sur une même droite, appelée axe de rotation.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Propriété

Dans le cas d'un mouvement de rotation uniforme, la vitesse d'un point \mathrm{M} à la surface de la sphère est constante et égale à : v=\omega \cdot r.
Le coefficient \omega, appelé vitesse angulaire, est égal \omega=\frac{2 \pi}{T} où T désigne la période de rotation de la sphère sur elle-même.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Questions

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 1

Un terrien se situant à l'équateur décrit une trajectoire circulaire par rapport au centre de la Terre. Il se situe à une distance R_{\mathrm{T}}=6~370 km du centre de sa trajectoire.

a. Exprimez la vitesse \mathrm{v} de ce terrien en fonction du rayon de la Terre R_{\mathrm{T}} et de la période de rotation de la planète \mathrm{T}.
b. Calculez la valeur de \mathrm{v}.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Exercice 2

À Paris, la distance de la tour Eiffel à son centre de trajectoire est égale à r=R_{\top} \cdot \cos (\varphi) où \varphi=48,9^{\circ}.

Calculez la vitesse \mathrm{v} de la tour Eiffel par rapport au centre de la Terre.
Afficher la correction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Exercice 3
La Lune présente toujours la même face par rapport à la Terre. Ce phénomène est dû au fait que sa rotation sur elle-même est synchronisée avec son mouvement de rotation autour de la Terre. On précise que la Lune met 27,3 jours pour faire son mouvement de rotation autour de la Terre et qu'elle se situe à 384 000 km de la Terre.

Calculez la vitesse \mathrm{v} du centre de la Lune par rapport au centre de la Terre.
Afficher la correction

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.