Chapitre 5
Exercices
Travailler les automatismes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
À l'oral
Envie de réaliser ces exercices à l'oral ? Enregistrez-vous !
Enregistreur audio
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1. Déterminer l'ensemble de définition.
2. Quelles limites peut-on conjecturer aux bornes de l'ensemble de définition ?
3. Quelles asymptotes éventuelles peut-on conjecturer ?
2. Quelles limites peut-on conjecturer aux bornes de l'ensemble de définition ?
3. Quelles asymptotes éventuelles peut-on conjecturer ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17

1.2.
1.3.

2.1.
2.2.
2.3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18

1.2.
1.3.

2.1.
2.2.
2.3.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Asymptotes
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
On donne ci-dessous la courbe représentative d'une fonction f définie sur \mathbb{R}.

2. Déterminer une équation de l'asymptote horizontale en -\infty et +\infty.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
On donne le tableau de variations d'une fonction g définie sur \mathbb{R}.

Déterminer à l'aide du tableau une équation des éventuelles asymptotes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
Soit f une fonction définie pour tout réel x \neq 2. On donne le tableau de variations suivant.

2. En déduire la présence d'une asymptote dont on donnera la nature et une équation.
3. Dans un repère orthogonal, tracer une allure possible de la courbe représentative de f.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Soit f une fonction définie sur un ensemble \mathcal{D}_{f}.
On note \mathcal{C}_{f} sa courbe représentative dans un repère orthogonal. 1. Au maximum, combien d'asymptotes horizontales \mathcal{C}_{f} peut-elle admettre ? Et d'asymptotes verticales ?
2. Trouver deux exemples permettant d'illustrer les réponses à la question précédente.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
À l'aide de la calculatrice, associer chaque courbe à une asymptote.
1. \mathcal{C}_{f} d'équation y=\frac{x+1}{x^{2}-3 x-5} ⟺
2. \mathcal{C}_{g} d'équation y=\frac{x^{3}}{2 x^{3}+x+1} ⟺
3. \mathcal{C}_{h} d'équation y=\frac{2 x^{4}+5}{x-3} ⟺
4. \mathcal{C}_{k} d'équation y=-4-\frac{x}{x^{2}+7} ⟺
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calculs de limites
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Déterminer la limite (éventuellement la limite à droite et la limite à gauche) de chaque fonction lorsque x tend vers a. 1. f: x \mapsto x^{3}+x-2 \:; a=-\infty
2. g: x \mapsto \sqrt{x} +\frac{1}{x} \:; a=+\infty
3. h: x \mapsto \frac{1}{\sqrt{x}+2}\:; a=+\infty
4. k: x \mapsto \frac{1}{x-2}\:; a=2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Déterminer la limite (éventuellement la limite à droite et la limite à gauche) de chaque fonction lorsque x tend vers a. 1. f: x \mapsto-\frac{3}{x^{2}+x}+5\:; a=+\infty
2. g: x \mapsto \frac{1}{x-4}+\sqrt{x}\:; a=4
3. h: x \mapsto \frac{1+\frac{1}{x}}{\sqrt{x-1}} ; a=+\infty
4. k: x \mapsto \frac{1}{x}+5 ; a=0
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
Déterminer les limites à gauche et à droite de chaque fonction lorsque x tend vers a.
1. f: x \mapsto \frac{x^{3}-2 x^{2}}{(x-1)^{2}}\:; a=1
2. g: x \mapsto \frac{5 x+2}{x+4}\:; a=-4
2. g: x \mapsto \frac{5 x+2}{x+4}\:; a=-4
3. h: x \mapsto \frac{1}{x^{2}-1}\:; a=-1
4. k: x \mapsto \frac{2}{\sqrt{x}-2}\:; a=4
4. k: x \mapsto \frac{2}{\sqrt{x}-2}\:; a=4
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Formes indéterminées
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
27
Déterminer les limites de chaque fonction en -\infty et en +\infty. 1. f: x \mapsto x^{2}-3 x+1
2. g: x \mapsto-x^{5}+10 x^{4}+x^{2}+x
3. h: x \mapsto \frac{x^{2}+2 x-3}{x+1}
4. k: x \mapsto \frac{3 x^{2}-1}{x^{2}-2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
28
Déterminer les limites de chacune des fonctions ci-après en -\infty et en +\infty. 1. f: x \mapsto 3 x^{4}-3 x^{2}+5 x+1
2. g: x \mapsto \frac{-x^{3}+x-1}{2 x+1}
3. h: x \mapsto \frac{4 x^{2}-3}{x^{7}-5 x^{4}+x^{2}+2 x-3}
4. k: x \mapsto \frac{x^{2}+x+1}{5 x^{2}+2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Théorèmes de comparaison et croissances comparées
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
29
Soit f une fonction définie sur \R vérifiant, pour tout réel x, x-2 \leqslant f(x) \leqslant x+2. Que peut-on en déduire pour les limites de f en +\infty et en -\infty ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
30
Soit g une fonction définie sur \R vérifiant, pour tout réel x non nul, 3-\frac{1}{x^{2}} \leqslant g(x) \leqslant 3+\frac{1}{x^{2}}. Que peut-on en déduire pour les limites de g en +\infty et en -\infty ? Et en 0 ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
31
On considère la fonction \ell définie sur \R par \ell(x)=\mathrm{e}^{x}+x-1. 1. Factoriser l'expression \ell(x) par \mathrm{e}^x.
2. Déterminer les limites de \ell en -\infty et +\infty.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
32
Déterminer les limites de chaque fonction en +\infty. 1. f: x \mapsto x^{2}+2 \cos (x)
2. g: x \mapsto \frac{\sin (x)}{x}
3. h: x \mapsto \frac{1}{\cos (x)+x}
4. k: x \mapsto \sqrt{x^{2}+2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
33
Déterminer les limites de chaque fonction en -\infty et en +\infty. 1. f: x \mapsto \frac{1}{\mathrm{e}^{x}+1}
2. g: x \mapsto \frac{\mathrm{e}^{x}+1}{x}
3. h: x \mapsto \mathrm{e}^{x}+2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
34
Les limites ci-dessous ont été calculées avec la fenêtre « Calcul formel » de GeoGebra. Justifier la réponse obtenue.
1. 
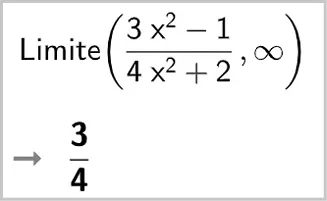
2.
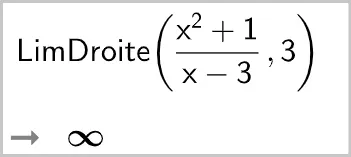

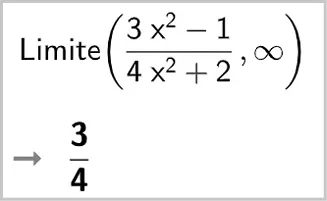
2.

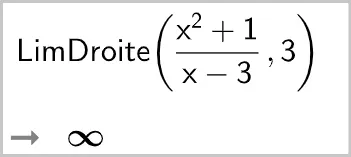
3. 
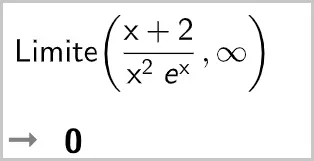
4.
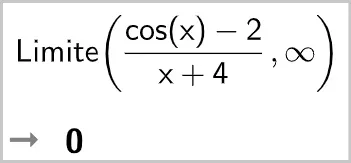

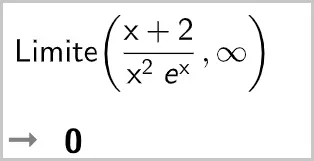
4.

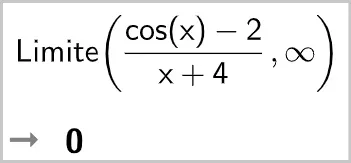
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exercices inversés
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
35
Déterminer une fonction f définie sur un ensemble de définition à préciser vérifiant \lim\limits_{\substack{x \to +\infty}}f(x)=3 et \lim\limits_{\substack{x \to 5}}f(x)=-\infty.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
36
Déterminer une fonction f dont la représentation graphique admet une asymptote d'équation y = 2 en -\infty mais pas d'asymptote en +\infty.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille


