Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 5
TP INFO 2
Limites et composées de fonctions
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Certaines fonctions étudiées au lycée ne peuvent s'écrire comme somme, produit ou quotient de fonctions de référence. Leurs limites éventuelles ne peuvent donc pas être déterminées à l'aide des théorèmes d'opérations sur les limites données dans le cours.
On s'intéresse à la fonction f définie sur ] 0 ;+\infty[ par f(x)=\sqrt{\frac{4 x+1}{x}} et à ses limites en 0 et en +\infty.
Questions préliminaires :
1. Quelles sont les fonctions de référence qui interviennent dans l'écriture de la fonction f ?
2. Justifier qu'il existe une fonction g, qu'on déterminera, telle que, pour tout x > 0, f(x)=\sqrt{g(x)}.
1. Quelles sont les fonctions de référence qui interviennent dans l'écriture de la fonction f ?
2. Justifier qu'il existe une fonction g, qu'on déterminera, telle que, pour tout x > 0, f(x)=\sqrt{g(x)}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Comprendre la construction de la fonction f et déterminer ses limites en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
On a f(x)=h(g(x)) pour tout x \in] 0 ;+\infty[ :
f est la composée de la fonction g par la fonction h.
On note aussi f=h \circ g. On peut démontrer le théorème suivant :
« Soient g et h deux fonctions. a, b et c sont des nombres réels ou +\infty ou -\infty.
Si \lim\limits_{\substack{x \to a}}g(x)=b et \lim\limits_{\substack{x \to b}}h(x)=c, alors \lim\limits_{\substack{x \to a}}h(g(x))=c. »
Si \lim\limits_{\substack{x \to a}}g(x)=b et \lim\limits_{\substack{x \to b}}h(x)=c, alors \lim\limits_{\substack{x \to a}}h(g(x))=c. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
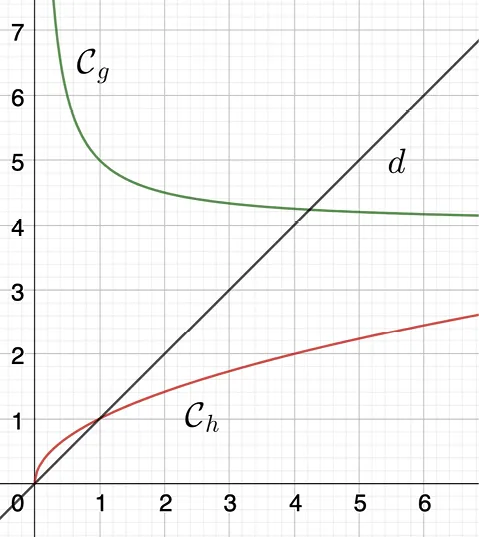
2. Tracer, sur le même graphique \mathcal{C}_{h}, la courbe représentative de la fonction h: x \mapsto \sqrt{x}.
3. Toujours sur le même graphique, tracer la droite d d'équation y = x.
4. a. Construire graphiquement l'image de 2 par la fonction g.
b. À l'aide de la droite d, construire graphiquement l'image de g(2) par la fonction h.
5. a. Créer un curseur a allant de 1 à 30 avec un pas de 1.
b. Créer le point \text{A} de coordonnées (a\:; g(a)).
c. Créer le point \text{B} de d d'abscisse g(a).
d. Créer la droite parallèle à l'axe des ordonnées passant par \text{B}. On appelle \text{C} le point d'intersection de cette droite et de \mathcal{C}_{h}.
e. Déplacer le curseur et observer le comportement du point \text{C}.
f. Que conjecturer pour la limite de f en +\infty ?
6. Conjecturer la limite de f en 0 en utilisant une méthode similaire.
f. Que conjecturer pour la limite de f en +\infty ?
6. Conjecturer la limite de f en 0 en utilisant une méthode similaire.
GeoGebra
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Tableur
1. Remplir la colonne A avec les nombres 1 à 50.
2. Quelle formule doit-on écrire dans la cellule B2 pour obtenir les images des nombres de la colonne A par la fonction g: x \mapsto \frac{4 x+1}{x} en faisant un copier-glisser ?
3. À l'aide de la fonction h: x \mapsto \sqrt{x}, remplir la colonne C pour trouver les images par la fonction f en utilisant les images par la fonction g de la colonne B.
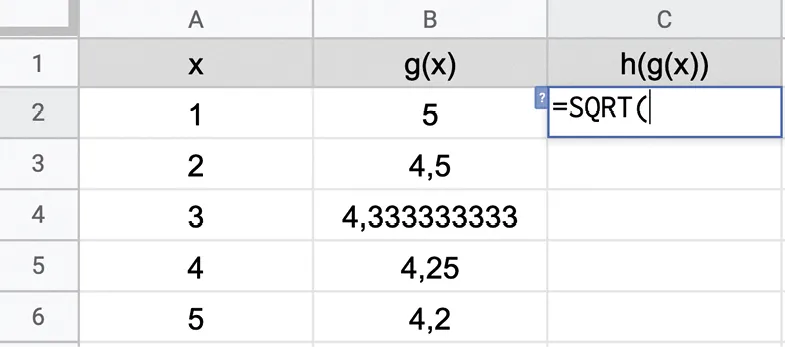
2. Quelle formule doit-on écrire dans la cellule B2 pour obtenir les images des nombres de la colonne A par la fonction g: x \mapsto \frac{4 x+1}{x} en faisant un copier-glisser ?
3. À l'aide de la fonction h: x \mapsto \sqrt{x}, remplir la colonne C pour trouver les images par la fonction f en utilisant les images par la fonction g de la colonne B.
4. Que peut-on conjecturer pour la limite de f en +\infty ?
5. Suivre la même démarche pour conjecturer la limite de f en 0.
5. Suivre la même démarche pour conjecturer la limite de f en 0.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah