Mathématiques Terminale Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Rappels de première
Algèbre et géométrie
Ch. 1
Combinatoire et dénombrement
Ch. 2
Vecteurs, droites et plans de l’espace
Ch. 3
Orthogonalité et distances dans l’espace
Analyse
Ch. 4
Suites
Ch. 5
Limites de fonctions
Ch. 6
Continuité
Ch. 7
Compléments sur la dérivation
Ch. 8
Logarithme népérien
Ch. 9
Fonctions trigonométriques
Ch. 10
Primitives - Équations différentielles
Ch. 11
Calcul intégral
Probabilités
Ch. 12
Loi binomiale
Ch. 13
Sommes de variables aléatoires
Ch. 14
Loi des grands nombres
Annexes
Exercices transversaux
Grand Oral
Apprendre à démontrer
Cahier d'algorithmique et de programmation
Chapitre 5
TP INFO 1
Étude de la propagation d'un virus
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Le 1er janvier, on constate que quelques habitants d'un village de 500 habitants sont infectés par un virus.
Puis, le virus se propage.

Voici le tableau donnant l'évolution du nombre total de personnes infectées dans le village.
On note \mathrm{N}(t) ce nombre en fonction du nombre t de jours depuis le 1er janvier jusqu'au 10 janvier.


Voici le tableau donnant l'évolution du nombre total de personnes infectées dans le village.
On note \mathrm{N}(t) ce nombre en fonction du nombre t de jours depuis le 1er janvier jusqu'au 10 janvier.
| t | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| \mathrm{N}(t) | 6 | 14 | 41 | 98 | 138 | 167 | 185 | 195 | 198 | 199 |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Prévoir si le virus va continuer à se propager dans le village et atteindre toute la population en utilisant une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1GeoGebra
1. En utilisant le tableau de valeurs ci-dessus, créer dix points de coordonnées (t\:; \mathrm{N}(t)) sur un graphique.
2. Créer trois curseurs : \text{K} entre \text{100} et \text{500} avec un pas de \text{1}, a entre \text{0} et \text{100} avec un pas de 1, et r entre 0 et 2 avec un pas de {0{,}1}.
3. Créer la fonction \mathrm{N}: t \mapsto \frac{\mathrm{K}}{1+a \mathrm{e}^{-r t}}.
4. Ajuster les curseurs \text{K}, r et a pour que la courbe suive au plus près les points. Noter ces valeurs.

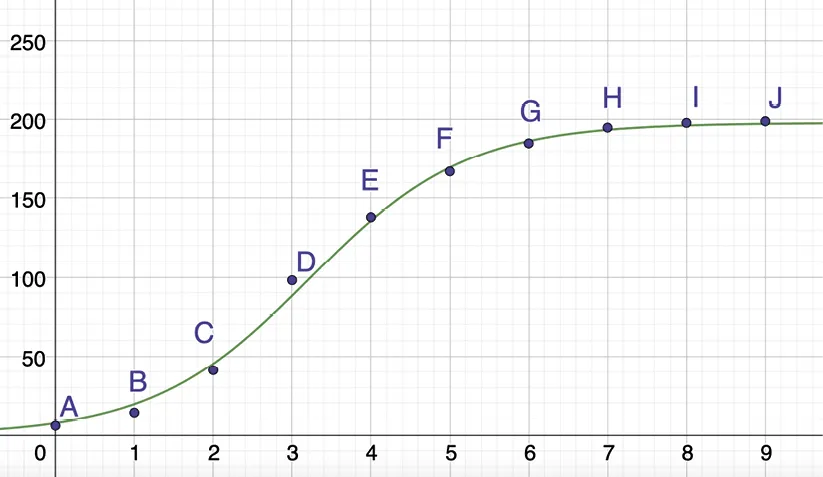
5. Par lecture graphique, préciser si tout le village va être infecté. Expliquer la démarche.
2. Créer trois curseurs : \text{K} entre \text{100} et \text{500} avec un pas de \text{1}, a entre \text{0} et \text{100} avec un pas de 1, et r entre 0 et 2 avec un pas de {0{,}1}.
3. Créer la fonction \mathrm{N}: t \mapsto \frac{\mathrm{K}}{1+a \mathrm{e}^{-r t}}.
4. Ajuster les curseurs \text{K}, r et a pour que la courbe suive au plus près les points. Noter ces valeurs.


5. Par lecture graphique, préciser si tout le village va être infecté. Expliquer la démarche.
6. Construire un outil géométrique permettant de déterminer graphiquement le moment où la vitesse de propagation est la plus élevée. Préciser la date approximative de ce moment.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Calculatrice
1. Dans le menu « Statistiques » de la calculatrice (ou dans le menu « Régression » pour les calculatrices NumWorks), entrer les données du tableau.
2. a. Dans ce menu, choisir la régression linéaire. Effectuer une régression linéaire en mathématiques revient à trouver une fonction affine qui permettra de s'approcher au mieux de la situation réelle observée.
b. Noter f la fonction déterminée par la calculatrice (arrondir les coefficients au dixième).
3. Recommencer avec une régression du second degré (fonction g), du troisième degré (fonction h), exponentielle (fonction \ell), puis logistique (fonction m).
2. a. Dans ce menu, choisir la régression linéaire. Effectuer une régression linéaire en mathématiques revient à trouver une fonction affine qui permettra de s'approcher au mieux de la situation réelle observée.
b. Noter f la fonction déterminée par la calculatrice (arrondir les coefficients au dixième).
3. Recommencer avec une régression du second degré (fonction g), du troisième degré (fonction h), exponentielle (fonction \ell), puis logistique (fonction m).
4. Tracer toutes ces fonctions sur le même écran de la calculatrice.
5. Quelles sont les modèles qui semblent suivre au mieux les points ?
6. En utilisant le contexte du problème d'épidémie, quel modèle faudrait-il garder ?
5. Quelles sont les modèles qui semblent suivre au mieux les points ?
6. En utilisant le contexte du problème d'épidémie, quel modèle faudrait-il garder ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
