Mathématiques 1re Spécialité
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 2
L'essentiel BAC
Fonctions de référence
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Fiche de révision
1 La fonction valeur absolue x \mapsto | x | est définie sur \mathbb { R } telle que pour tout x \lt 0 , | x | = - x et pour tout x \geqslant 0 , | x | = x. Cette fonction est décroissante sur ] - \infty \: ; 0 ] et croissante sur [ 0 \: ; + \infty [. Cela permet de :
✔ résoudre des problèmes en lien avec des distances entre nombres réels ;✔ écrire des inégalités ou des égalités à l'aide de la valeur absolue.
2 Une fonction polynôme du second degré est définie sur \mathbb { R } et s'écrit sous la forme x \mapsto a x ^ { 2 } + b x + c où a, b et c sont des réels tels que a \neq 0. Les variations d'une fonction polynôme dépendent du signe de a et un extremum est toujours atteint pour x = \dfrac { -b } { 2 a }. Cela permet de :
✔ étudier des fonctions faisant intervenir la fonction carré ;✔ résoudre des problèmes liés à la physique ;
✔ résoudre des problèmes d'optimisation.
3 Une fonction polynôme du second degré est représentée par une parabole qui possède un axe de symétrie. Cela permet de :
✔ retrouver l'expression d'une fonction polynôme à partir des informations graphiques ;✔ construire une allure de parabole respectant des contraintes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Carte mentale

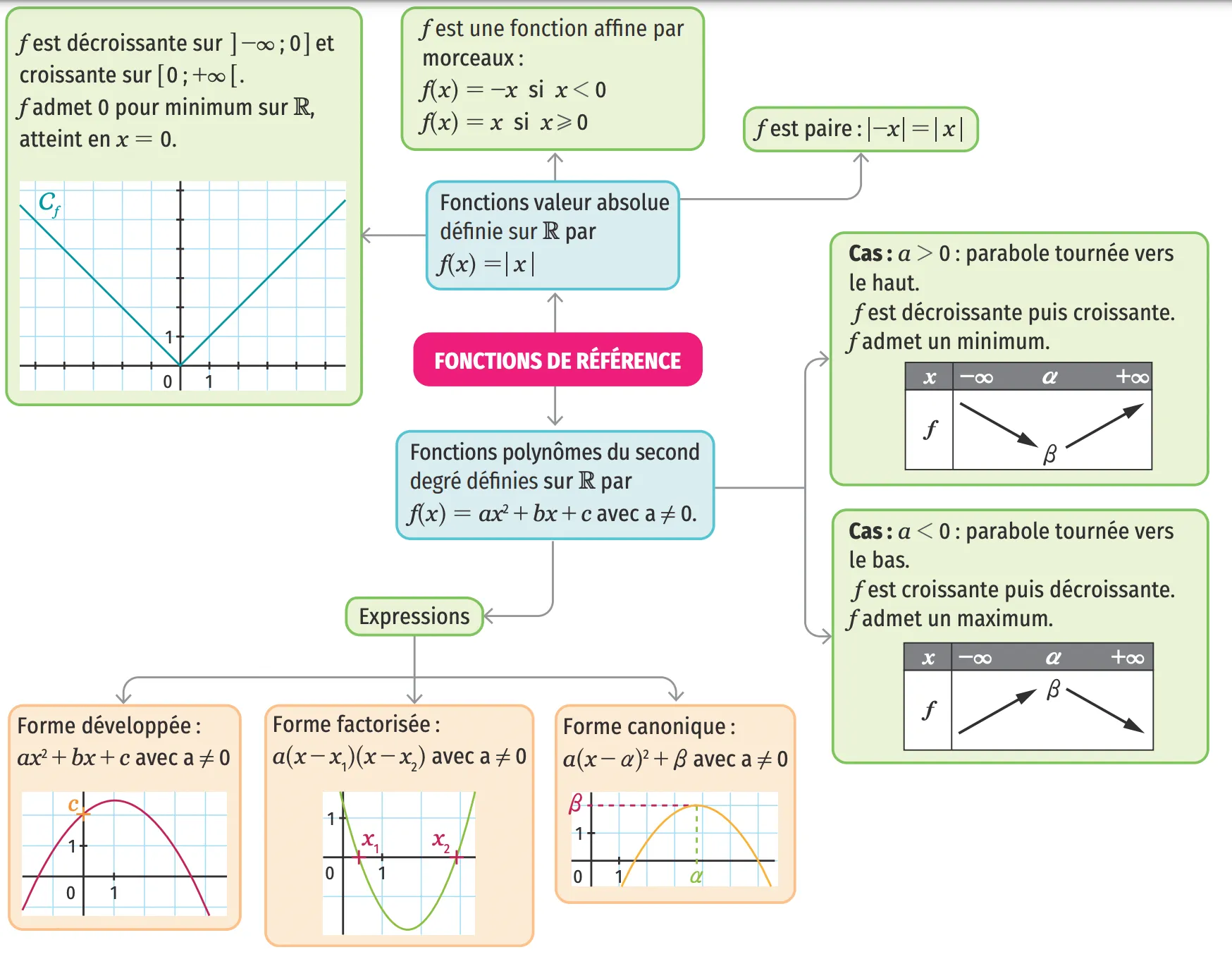
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
