Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algèbre
Ch. 1
Suites numériques
Ch. 2
Fonctions de référence
Ch. 3
Équations et inéquations du second degré
Analyse
Ch. 4
Dérivation
Ch. 5
Applications de la dérivation
Ch. 6
Fonction exponentielle
Ch. 7
Trigonométrie
Ch. 8
Fonctions trigonométriques
Géométrie
Ch. 9
Produit scalaire
Ch. 10
Configurations géométriques
Probabilités et statistiques
Ch. 11
Probabilités conditionnelles
Ch. 12
Variables aléatoires réelles
Annexes
Exercices transversaux
Cahier d'algorithmique et de programmation
Rappels de seconde
Chapitre 9
TP / TICE 2
Travail d'une force
15 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Énoncé
Dans un jardin d'enfants, on souhaite construire un toboggan. Pour cela, on modélise sa forme dans un repère orthogonal (\text{O}\, ; \vec{i}, \vec{j}) à l'aide de la courbe représentative \mathcal{C} (en vert) de la fonction f définie sur [0\, ; 2] par f(x) = 0{,}3x^3 - 0{,}9x^2 + 1{,}2 .
On néglige tous les frottements et on rappelle que le poids de l'enfant \overrightarrow{\mathrm{P}} est colinéaire à \vec{j} et dans le sens de -\vec{j} avec \|\overrightarrow{\mathrm{P}}\| = mg et {g = 9{,}81} m·s–2.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Questions préliminaires
On divise l'intervalle [0\, ; 2] en deux intervalles identiques et on place trois points \mathrm{A}_0 , \mathrm{A}_1 et \mathrm{A}_2 sur \mathcal{C} tels que x_{\text{A}_0}=0, x_{\text{A}_1}=1 et x_{\text{A}_2}=2.
Le travail du poids de l'enfant lorsqu'il parcourt le segment \left[\mathrm{A_0 A_1}\right] est donné en joule par \overrightarrow{\text{P}} \cdot \overrightarrow{\mathrm{A_0A_1}}. Le travail total est la somme du travail sur chaque intervalle. Dans ce cas on a donc \text{W} = \overrightarrow{\text{P}} \cdot \overrightarrow{\mathrm{A_0A_1}} + \overrightarrow{\text{P}} \cdot \overrightarrow{\mathrm{A_1A_2}}. 1. Calculer les coordonnées des vecteurs \overrightarrow{\mathrm{A}_{0} \mathrm{A}_{1}}, \overrightarrow{\mathrm{A}_{1} \mathrm{A}_{2}} et \overrightarrow{\mathrm{P}} sachant que m = 20 kg.
2. En déduire la valeur de \text{W.}
3. On admet que \mathrm{W}=\dfrac{1}{2} m v^{2} où v est la vitesse de l'enfant en m·s–1 à la fin de la descente. Calculer la valeur de v .
Le travail du poids de l'enfant lorsqu'il parcourt le segment \left[\mathrm{A_0 A_1}\right] est donné en joule par \overrightarrow{\text{P}} \cdot \overrightarrow{\mathrm{A_0A_1}}. Le travail total est la somme du travail sur chaque intervalle. Dans ce cas on a donc \text{W} = \overrightarrow{\text{P}} \cdot \overrightarrow{\mathrm{A_0A_1}} + \overrightarrow{\text{P}} \cdot \overrightarrow{\mathrm{A_1A_2}}. 1. Calculer les coordonnées des vecteurs \overrightarrow{\mathrm{A}_{0} \mathrm{A}_{1}}, \overrightarrow{\mathrm{A}_{1} \mathrm{A}_{2}} et \overrightarrow{\mathrm{P}} sachant que m = 20 kg.
2. En déduire la valeur de \text{W.}
3. On admet que \mathrm{W}=\dfrac{1}{2} m v^{2} où v est la vitesse de l'enfant en m·s–1 à la fin de la descente. Calculer la valeur de v .
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Objectif
Approcher la courbe avec une subdivision plus précise et étudier le travail du poids à l'aide d'une des deux méthodes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 1Tableur
1. On commence par diviser l'intervalle [0\, ; 2] en dix intervalles égaux pour obtenir dix segments approchant la courbe de f .
a. Créer une feuille de calcul contenant dans les colonnes A et B les coordonnées des points \text{A}_0, \text{A}_1, …, \text{A}_{10} ainsi créés.
b. Dans les colonnes C et D, calculer les coordonnées des vecteurs \overrightarrow{\mathrm{A}_{0} \mathrm{A}_{1}}, \overrightarrow{\mathrm{A}_{1} \mathrm{A}_{2}}, \ldots, \overrightarrow{\mathrm{A}_{9} \mathrm{A}_{10}}.
c. Dans les colonnes E et F, recopier 10 fois les coordonnées du vecteur \overrightarrow{\mathrm{P}}.
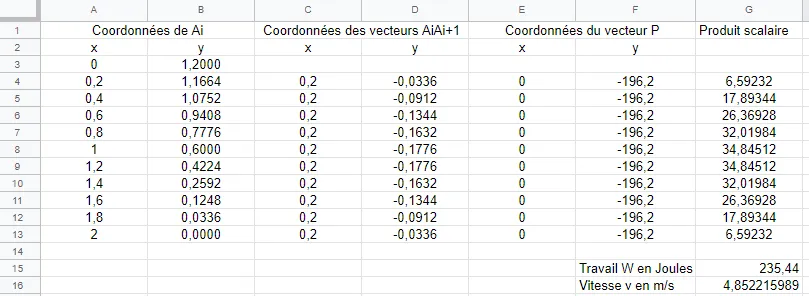d. Dans la colonne G calculer le produit scalaire \overrightarrow{\mathrm{A}_{i} \mathrm{A}_{i+1}} \cdot \overrightarrow{\mathrm{P}}.
e. En déduire enfin la valeur de \mathrm{W} puis celle de v . Que constate-t-on par rapport aux questions préliminaires ?
a. Créer une feuille de calcul contenant dans les colonnes A et B les coordonnées des points \text{A}_0, \text{A}_1, …, \text{A}_{10} ainsi créés.
b. Dans les colonnes C et D, calculer les coordonnées des vecteurs \overrightarrow{\mathrm{A}_{0} \mathrm{A}_{1}}, \overrightarrow{\mathrm{A}_{1} \mathrm{A}_{2}}, \ldots, \overrightarrow{\mathrm{A}_{9} \mathrm{A}_{10}}.
c. Dans les colonnes E et F, recopier 10 fois les coordonnées du vecteur \overrightarrow{\mathrm{P}}.
Cliquez ici pour avoir accès à une correction
Le zoom est accessible dans la version Premium.
e. En déduire enfin la valeur de \mathrm{W} puis celle de v . Que constate-t-on par rapport aux questions préliminaires ?
2. Refaire les mêmes étapes avec, cette fois, une subdivision en 50 intervalles (et donc 51 points créés). Que constate-t-on ?
3. Reprendre les mêmes étapes mais avec la fonction g définie sur [0\, ; 2] par g(x)=-0\text{,}3 x^{2} \times \mathrm{e}^{-x+2}+1\text{,}2.
Que constate-t-on ? Cela paraît-il sensé ? Quelle hypothèse très forte du départ fausse la modélisation ?
3. Reprendre les mêmes étapes mais avec la fonction g définie sur [0\, ; 2] par g(x)=-0\text{,}3 x^{2} \times \mathrm{e}^{-x+2}+1\text{,}2.
Que constate-t-on ? Cela paraît-il sensé ? Quelle hypothèse très forte du départ fausse la modélisation ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Méthode 2Python
1. On commence par diviser l'intervalle [0\, ; 2] en dix intervalles égaux pour obtenir dix segments approchant la courbe de f . On crée ainsi onze points \mathrm{A}_0, \mathrm{A}_1, …, \mathrm{A}_{10}.
Exprimer les coordonnées du vecteur \overrightarrow{\mathrm{A}_{i} \mathrm{A}}_{i+1} en fonction de i \in\{0 \: ; 1 \: ; \ldots \: ; 9\}.
2. a. Compléter la ligne 2 dans le code ci-dessous afin de créer une fonction f qui renvoie l'image de x par la fonction f .
2. a. Compléter la ligne 2 dans le code ci-dessous afin de créer une fonction f qui renvoie l'image de x par la fonction f .
def f(x): return(...) x = 0 n = 10 k = 2/n W = 0 for i in range(n): PS = -196.2 * (f(x+k) - f(x)) W = W + PS x = x + k
Cliquez pour accéder à la correction
b. Comment peut-on expliquer le code à partir de la ligne 3, notamment la variable PS ?
3. Faire afficher la valeur de \text{W} lorsque n = 10 et calculer la valeur de v . Que constate-t-on par rapport aux questions préliminaires ?
4. Faire des tests avec différentes valeurs de n de plus en plus grandes et commenter les résultats.
5. Reprendre ce programme mais avec la fonction g définie sur [0\, ; 2] par g(x)=-0\text{,}3 x^{2} \times \mathrm{e}^{-x+2}+1\text{,}2. Que constate-t-on ? Cela paraît-il sensé ? Quelle hypothèse très forte du départ fausse la modélisation ?
3. Faire afficher la valeur de \text{W} lorsque n = 10 et calculer la valeur de v . Que constate-t-on par rapport aux questions préliminaires ?
4. Faire des tests avec différentes valeurs de n de plus en plus grandes et commenter les résultats.
5. Reprendre ce programme mais avec la fonction g définie sur [0\, ; 2] par g(x)=-0\text{,}3 x^{2} \times \mathrm{e}^{-x+2}+1\text{,}2. Que constate-t-on ? Cela paraît-il sensé ? Quelle hypothèse très forte du départ fausse la modélisation ?
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah