Mathématiques 4e - 2022
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algorithmique et programmation
Dossier Scratch
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d'équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Prolongement
Chapitre 14
Exercices
Calculs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calcul mental
Sans calculatrice, ni crayon
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
15
Calculer mentalement les expressions suivantes.
1. 4 \times 7 \times 5
2. 2 \times 6 \times 9,5
3. \frac{2}{3} \times \frac{4}{5} \times \frac{25}{16}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
16
Effectuer les conversions de volumes suivants.
1. 1\mathrm{~m}^{3}~=~ \mathrm{cm}^{3}
2. 230\mathrm{~mm}^{3}~=~ \mathrm{cm}^{3}
3. 234~500~\mathrm{dm}^{3}~=~ \mathrm{m}^{3}
2. 230\mathrm{~mm}^{3}~=~
3. 234~500~\mathrm{dm}^{3}~=~
4. 0,07~\mathrm{dam}^{3}~=~ \mathrm{m}^{3}
5. 18\mathrm{~cm}^{3}~=~ \mathrm{dm}^{3}
6. 680~000~000\mathrm{~m}^{3}~=~ \mathrm{km}^{3}
5. 18\mathrm{~cm}^{3}~=~
6. 680~000~000\mathrm{~m}^{3}~=~
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
17
Effectuer les conversions d'aires suivantes.
1. 123~\mathrm{m}^{3}=~ \mathrm{dm}^{2}
2. 450~000~\mathrm{mm}^{2}=~ \mathrm{m}^{2}
3. 700~\mathrm{dm}^{3}=~ \mathrm{cm}^{2}
2. 450~000~\mathrm{mm}^{2}=~
3. 700~\mathrm{dm}^{3}=~
4. 0,004~\mathrm{m}^{2}=~ \mathrm{cm}^{2}
5. 130~\mathrm{km}^{2}=~ \mathrm{hm}^{2}
6. 0,012~\mathrm{hm}^{2}=~ \mathrm{dam}^{2}
5. 130~\mathrm{km}^{2}=~
6. 0,012~\mathrm{hm}^{2}=~
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
18
Effectuer les conversions de volumes suivants.
1. 31~\mathrm{dL}=~ \mathrm{cL}
2. 120~\mathrm{L}=~ \mathrm{daL}
3. 0,03~\mathrm{hL}=~ \mathrm{L}
2. 120~\mathrm{L}=~
3. 0,03~\mathrm{hL}=~
4. 150~\mathrm{mL}=~ \mathrm{cL}
5. 4~500~\mathrm{mL}=~ \mathrm{daL}
6. 56~\mathrm{dL}=~ \mathrm{daL}
5. 4~500~\mathrm{mL}=~
6. 56~\mathrm{dL}=~
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
19
Soit \text{SABC} une pyramide dont la base est un triangle équilatéral de \text{7~cm} de côté et dont les faces latérales sont toutes des triangles isocèles égaux tel que \text{SA~=~4,5~cm}.
Calculer la somme des longueurs de toutes les arêtes de cette pyramide.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calcul posé
Sur feuille en posant les calculs
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
20
Calculer les aires de ces triangles. Les longueurs sont données en cm.


Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
21
1. Calculer 5,3\times3,2\times 6,5.
2. Calculer 12,4\times4\times 0,33.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
22
Compléter les tableaux de proportionnalité suivants.
| Angle | Longueur de l'arc de cercle |
|---|---|
| 360^{\circ} | \text{240~cm} |
| 60^{\circ} |
| Angle | Longueur de l'arc de cercle |
|---|---|
| 360^{\circ} | \text{75~cm} |
| \text{25~cm} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Calcul instrumenté
Avec la calculatrice ou l'ordinateur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
23
Donner la valeur exacte puis une valeur approchée au dixième près de l'aire d'un disque de rayon \text{5~cm}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
24
Donner la valeur exacte puis une valeur approchée au centième près de l'aire d'un disque de diamètre \text{6,3~cm}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
25
Donner une valeur approchée arrondie à l'unité près des calculs suivants.
1. \frac{2,5 \times 6,2}{3}
2. \frac{29 \times 130}{3}
2. \frac{29 \times 130}{3}
3. \frac{14 \pi \times 6}{3}
4. \frac{0,12 \pi \times 1,4}{3}
4. \frac{0,12 \pi \times 1,4}{3}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
26
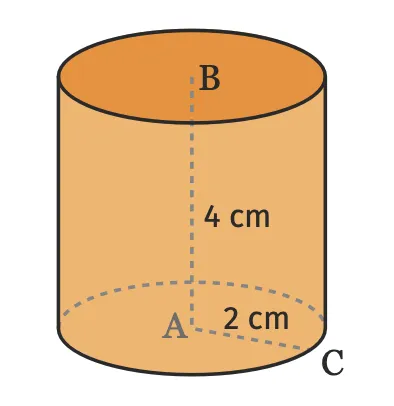
Julia trouve dans son cahier de 5e la formule pour calculer le volume d'un cylindre : \pi \times \text {rayon}^{2} \times \text {hauteur}.
Aider Julia à donner une valeur du volume du cylindre suivant arrondie à l'unité près.

Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
