Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Algorithmique et programmation
Dossier Scratch
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d'équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Prolongement
Chapitre 14
Exercices d'entraînement
1 - Pyramides
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vérifier que les connaissances de base sont acquises.
Développer les connaissances.
Maîtriser les notions de manière approfondie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pour les exercices 46 et 47
On utilisera le pavé droit \text{ABCDEFGH} suivant.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
46
[Rep.7]
1. Citer une pyramide à base rectangulaire
ayant pour hauteur [\mathrm{HE}].
2. Citer une pyramide à base triangulaire ayant pour hauteur [\mathrm{HE}].
2. Citer une pyramide à base triangulaire ayant pour hauteur [\mathrm{HE}].
3. Citer trois pyramides ayant pour base le
triangle \text{ADC}.
4. Citer trois pyramides ayant pour base le triangle \text{GHD}.
4. Citer trois pyramides ayant pour base le triangle \text{GHD}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
47
[Rep.7 - Com.4]
Compléter le tableau suivant.| Pyramide | Sommet | Base | Hauteur |
|---|---|---|---|
| \text{FEABC} | |||
| \text{FGCBD} | |||
| \text{EFGHA} |
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
48
[Rep.3 - Rep.7]
Les figures suivantes sont des patrons de pyramide dont la base est colorée.Pour chacun de ces patrons, réaliser à main levée une représentation en perspective cavalière de la pyramide qu'il représente.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
49
[Rep.3 - Rep.7]
\text{ABCDEFGH} est un
cube de \text{5~cm} de côté.
1. Construire un patron du tétraèdre \text{GDAH}.
Cliquez pour accéder à une zone de dessin
2. Construire un patron du tétraèdre \text{EGBF}.
Cliquez pour accéder à une zone de dessin
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
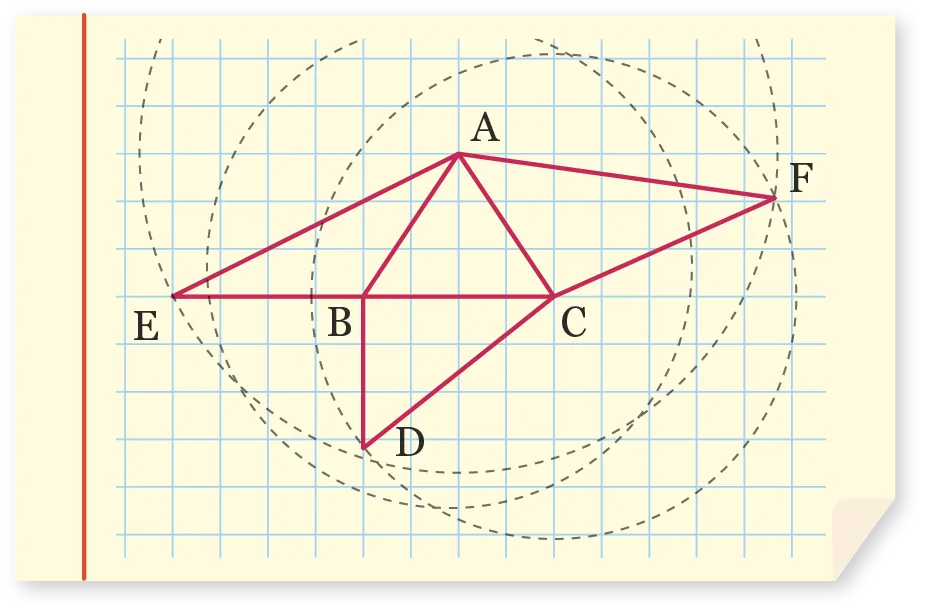
50Copie d'élève[Rais.5 - Com.2]
Valentin a réalisé sur une feuille de
papier la figure suivante dans le but de construire une pyramide dont la base est
un triangle isocèle. Son professeur lui dit
que son dessin ne pourra pas donner le résultat escompté.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
51[Cal.5 - Ch.1]
La pyramide de Khéops est le monument emblématique de l'Antiquité égyptienne, construite vers 2560 av. J.-C. Il s'agit d'une pyramide dont la base est un carré de 440 coudées royales de côté et sa hauteur est d'environ 280 coudées royales. Sachant qu'une coudée royale est équivalente à environ
\text{52~cm}, donner le volume, arrondi au \text{m}^{3} près de cette pyramide.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
52[Cal.4 - Ch.1]
On considère la figure de l'exercice 49
. Calculer le volume des tétraèdres \text{GDAH} et \text{EGBF}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
53Démo[Rais.4 - Rep.7 - Mod.8]
Soit \text{ABCDEFGH} un cube de côté c dans lequel on découpe trois pyramides \text{CEFGH}, \text{HABCD} et \text{CABFE}.
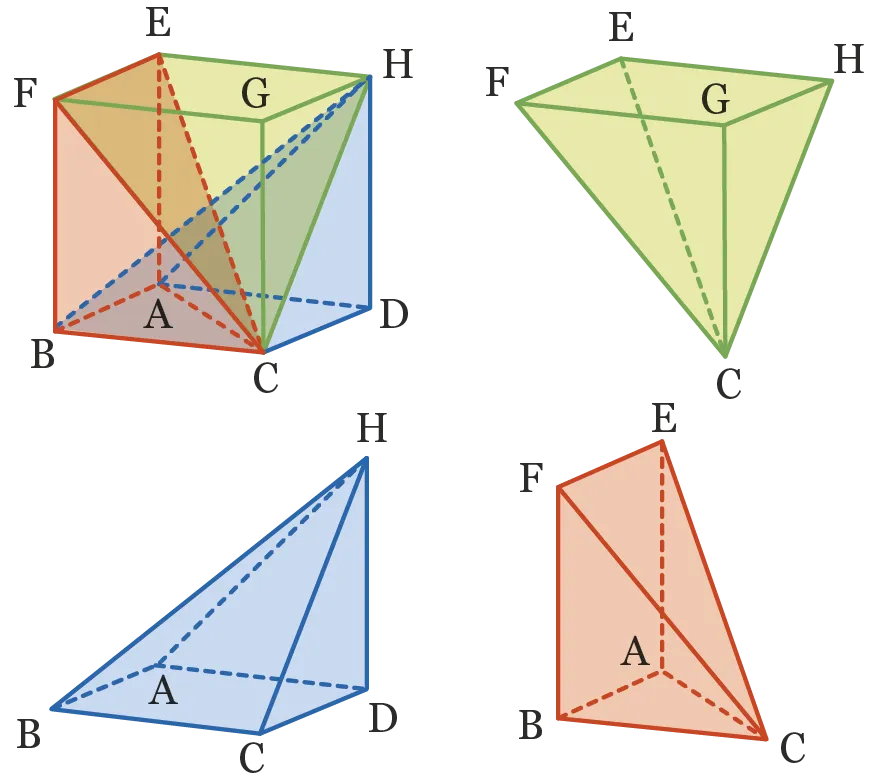
1. Pour chaque pyramide donner le nom de la base et sa nature, ainsi que le nom de la hauteur.
2. Que peut-on dire des trois pyramides ?
2. Que peut-on dire des trois pyramides ?
3. Exprimer le volume du cube en fonction de c.
4. Démontrer que le volume d'une des pyramides se calcule par la formule :
\text {Volume}=\frac{\text {aire de la base} \times \text {hauteur}}{3}.
4. Démontrer que le volume d'une des pyramides se calcule par la formule :
\text {Volume}=\frac{\text {aire de la base} \times \text {hauteur}}{3}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah