Mathématiques 4e - 2022
Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Mes Pages
Algorithmique et programmation
Dossier Scratch
Partie 1 : Nombres et calculs
Ch. 1
Nombres relatifs
Ch. 2
Addition et soustraction de nombres rationnels
Ch. 3
Multiplication et division de nombres rationnels
Ch. 4
Puissances
Ch. 5
Calcul littéral
Ch. 6
Résolution d'équations
Partie 2 : Organisation et gestion de données, fonctions
Ch. 7
Statistiques
Ch. 8
Probabilités
Ch. 9
Notion de fonctions
Ch. 10
Proportionnalité
Partie 3 : Espace et géométrie
Ch. 11
Théorème de Thalès
Ch. 12
Propriétés des triangles rectangles
Ch. 13
Géométrie plane
Ch. 14
Géométrie dans l'espace
Prolongement
Chapitre 12
Exercices d'entraînement
1 - Le théorème de Pythagore
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Vérifier que les connaissances de base sont acquises.
Développer les connaissances.
Maîtriser les notions de manière approfondie.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
58[Mod.4 - Com.4]
Associer chaque proposition avec celle qui lui correspond.
\text{AB}^{2}=\text{AC}^{2}+\text{BC}^{2}
\text{EF}^{2}+\text{EG}^{2}=\text{FG}^{2}
\text{AB}^{2}+\text{BC}^{2}=\text{AC}^{2}
\text{EF}^{2}+\text{EG}^{2}=\text{FG}^{2}
\text{AB}^{2}+\text{BC}^{2}=\text{AC}^{2}
\text{EG}^{2}=\text{EF}^{2}+\text{FG}^{2}
\text{EF}^{2}=\text{GE}^{2}+\text{GF}^{2}
\text{BC}^{2}=\text{AB}^{2}+\text{AC}^{2}
\text{EF}^{2}=\text{GE}^{2}+\text{GF}^{2}
\text{BC}^{2}=\text{AB}^{2}+\text{AC}^{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
59[Rep.6 - Mod.4]
Dans le triangle \text{BCV} rectangle en \text{B}, on a \text{BV = 8,4~cm} et \text{BC = 1,3~cm}.1. Quelle est l'hypoténuse du triangle \text{BCV} ?
Cliquez pour accéder à une zone de dessin
3. Calculer la longueur \text{CV}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
60[Rep.6 - Mod.4]
Dans le triangle \text{JFD} rectangle en \text{F}, on a
\text{JD = 5,2~dm} et \text{JF = 45~cm}.1. Réaliser une figure à main levée.
Cliquez pour accéder à une zone de dessin
2. Calculer la longueur \text{FD} arrondie au millimètre près.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
61[Ch.2 - Rais.3]
Un toboggan est fabriqué tel que l'échelle soit
perpendiculaire à la rampe.L'échelle mesure \text{2~m} et l'écartement entre les deux extrémités \text{A} et \text{C} du toboggan est de \text{9~m}. Quelle est la longueur, arrondie au cm près, de la rampe ?

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
62Démo[Ch.2 - Rais.3 - Rais.4]
\text{ABC} est un triangle rectangle en \text{C}.
On va démontrer le théorème de Pythagore. On note {\text{AB = } c}, {\text{AC = }b} et {\text{BC = }a}.La figure suivante est composée du triangle \text{ABC} et de trois autres triangles identiques à \text{ABC} où \text{A}, \text{B}, \text{E} et \text{H} appartiennent respectivement à \text{[FC]}, \text{[CD]}, \text{[DG]}, et \text{[GF]}.
1. Coder la figure.
2. Déterminer la nature de \text{CFGD}.
2. Déterminer la nature de \text{CFGD}.
3. Démontrer que \widehat\text{ABE} est un angle droit. En déduire la nature de \text{ABEH} et déterminer une expression de son aire en fonction de c.

a. Déterminer l'aire du carré \text{AJKF} et celle du carré \text{BDIJ} en fonction de a et b.
b. Justifier que
\text{Aire(AJKF)} \text{+ Aire(BDIJ)} \text{= Aire(ABEH)} où \text{ABEH} est le carré de la figure initiale.
c. En déduire une relation entre a, b et c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
63[Ch.2 - Com.4 - Mod.4]
Dans la figure suivante, les points \text{B}, \text{G} et \text{F} sont alignés. On donne \text{BG = 3~cm}, \text{BD = 5~cm,} \text{DF = 13~cm.}

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
64[Ch.1 - Ch.2]
Un circuit de courses a la forme du tracé suivant (le dessin n'est pas à l'échelle).On doit faire sept tours complets de ce circuit passant par \text{D,} \text{F,} \text{H,} \text{G,} \text{F,} \text{E} et finissant par \text{D}.

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
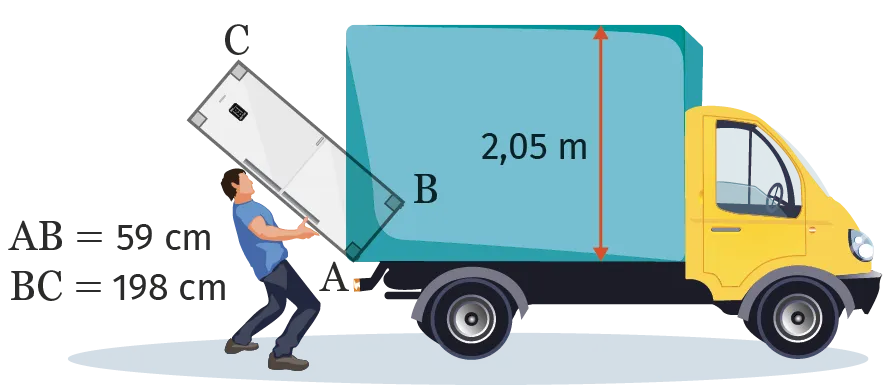
65[Ch.2 - Rais.2 - Rais.3] D'après Brevet, Nouvelle-Calédonie, 2018
Lors de son déménagement, Basile doit transporter son réfrigérateur dans un camion. Pour l'introduire dans le camion, Basile le pose sur le bord comme indiqué sur la figure. Le schéma n'est pas à l'échelle.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
