Nos classiques

Guide CP-Maths

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
I
Présentation
II
Liaison grande section - CP
Période 1
1- Suite orale des nombres jusqu’à 30
Numérationp. 28-29
2- Comparer des quantités jusqu’à 19
Numérationp. 30-32
3- Suite écrite des nombres jusqu’à 19
Numérationp. 33-35
4- Ajouter des nombres, découvrir les signes + et =
Calculp. 36-40
5- Tracer à la règle
Géométriep. 41-43
6- Comparer et ordonner des nombres jusqu’à 19
Numérationp. 44-45
7- Décomposer les nombres jusqu’à 9
Calculp. 46-48
8- Indiquer un rang et une position jusqu’à 10
Numérationp. 49-50
9- Dizaines-unités : grouper pour comparer
Numérationp. 51-55
10- Table d’addition : les compléments à 10
Calculp. 56-58
11- Construire la droite graduée
Numérationp. 59-63
12- Table d'addition : ajouter 10
Calculp. 64-65
Problèmes de type partie-tout : recherche du tout
Problèmesp. 66-68
Problèmes équivalents à la recherche d’un tout
Problèmesp. 69-71
Problèmes en plein air
Problèmesp. 72-73
Séances supplémentaires
Exercicesp. 74-75
Période 2
Période 3
Période 4
Période 5
Annexes
Numération
Séquence 11

Construire la droite graduée

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour Schéma: séquences d'apprentissage sur l'addition, la soustraction et les nombres précédents/suivants.Schéma: séquences d'apprentissage sur l'addition, la soustraction et les nombres précédents/suivants.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Objectif de la séquence

  • Découvrir et utiliser la droite graduée
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Conseil didactique

La droite graduée est une représentation qui permet de faire le lien entre l'aspect cardinal du nombre, c'est-à-dire le nombre d'éléments d'une collection, et son aspect ordinal. Elle donne aussi à voir le lien entre numération et géométrie en donnant du sens à certaines expressions, comme « 39 est proche de 40 » ou « 21 est entre 20 et 22 ». Cette première forme de modélisation pourra être utilisée par les élèves tout au long de leur scolarité, pour représenter les nombres et pour calculer. Cette approche est à préférer dès le CP à la « frise numérique » afin de donner le temps aux élèves de s'approprier cet outil.
Plus d'explications en
vidéo
.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 3
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Séance 1
60 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Problèmes du jour
Individuel
10 min

Problèmes additifs : recherche du tout

Problème 1

Je me demande combien il y a d'oiseaux en tout sur la branche. Il y avait 2 oiseaux et 6 les ont rejoints.
Retrouvez ce problème au format
numérique
.

Problème 2

Il y avait 6 personnes dans le bus. 4 personnes les rejoignent.
Combien y a-t-il de personnes dans le bus ?
Retrouvez ce problème au format
numérique
.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Rituel de calcul
Collectif puis en binômes
10 min

Jeu des illusions

Faire une partie collective du jeu des illusions (voir
séquence 7 p. 46
) avec 5 jetons, puis réaliser collectivement la maison du 5.
Ensuite, faire jouer les élèves en binômes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Apprentissage
40 min

Objectif de la séance
  • Découvrir la droite graduée
Matériel de la séance
  • 20 cubes par binôme
  • 1 feuille A3 par binôme
  • Ressources numériques à projeter
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Entrée dans l'activité
Collectif
2 min

Demander aux élèves de rappeler les activités réalisées avec la tour d'appel si elle a été proposée en début d'année. « Aujourd'hui, nous allons préparer des suites de cubes et nous allons découvrir un outil très pratique pour trouver combien il y a de cubes sans les compter : la droite graduée. »
Placeholder pour Illustration : étoile jaune souriante tenant une cible avec une flèche au centre.Illustration : étoile jaune souriante tenant une cible avec une flèche au centre.
Découvrir la droite graduée.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Découverte de la droite graduée
Collectif
10 min

Constituer un emboitement de 10 cubes devant les élèves. Expliquer : « Je vais tracer la droite graduée qui correspond à mon emboitement de cubes. »

Pour cette étape, utiliser l'outil « Droite graduée » pour projeter les cubes. Il est également possible d'utiliser de gros cubes du commerce.

Tracer une ligne horizontale au tableau.

Placeholder pour Image abstraite : carré jaune sur plateforme noire, fond vert.Image abstraite : carré jaune sur plateforme noire, fond vert.

Aligner un cube avec le début de la ligne, placer deux graduations en traçant un trait vertical à chaque arête du premier cube. Dire : « Je marque avec un trait où commence ma suite de cubes, puis je marque la longueur du premier cube. »

Placeholder pour Illustration : conteneur jaune sur plateforme, fond vert.Illustration : conteneur jaune sur plateforme, fond vert.

Placer un second cube à côté du premier et marquer la graduation. Dire : « Je trace un nouveau trait pour marquer l'espace occupé par le cube. »

Placeholder pour Illustration : panneau rectangulaire jaune à 12 cases, surmonté d'une barre noire et posé sur pieds.Illustration : panneau rectangulaire jaune à 12 cases, surmonté d'une barre noire et posé sur pieds.

Procéder de la même manière jusqu'à avoir placé une vingtaine de cubes.

Placeholder pour Diagramme linéaire : ligne horizontale avec 13 marqueurs.Diagramme linéaire : ligne horizontale avec 13 marqueurs.

Retirer les cubes et observer la droite graduée obtenue.

Expliquer que les traits s'appellent des graduations.

Placeholder pour Diagramme: segment de 0 à 1, divisé en 16 parties égales.Diagramme: segment de 0 à 1, divisé en 16 parties égales.

Montrer l'espace entre les deux premières graduations, et écrire « 0 » et « 1 » sous les graduations correspondantes. Expliquer : « Ici, on n'avait pas de cube, on écrit "0". Ici il y avait un cube, on a donc la longueur d'un cube, on écrit "1" sous la graduation. »

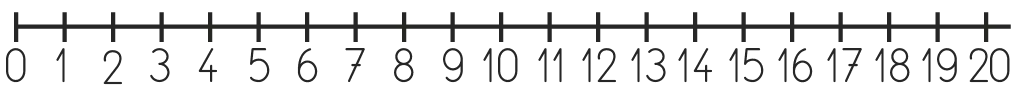
Placeholder pour Illustration : règle graduée de 0 à 20Illustration : règle graduée de 0 à 20

Poursuivre en écrivant les nombres suivants sous les graduations et en montrant à chaque fois les intervalles : « Puis il y avait un autre cube ici, cela fait 2 cubes. On a donc la longueur de 2 cubes. » Continuer de la même manière pour les graduations suivantes, jusqu'à écrire « 20 ».


« Cette représentation s'appelle la droite graduée. Entre chaque nombre, nous avions un cube (montrer différents intervalles). Les graduations, elles, nous permettent de trouver très rapidement combien il y a de cubes en les plaçant sur la droite : il suffit ensuite de lire le nombre sur lequel se termine notre emboitement. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Tracer la droite graduée à deux
En binômes
10 min

« À votre tour, vous allez préparer une droite graduée par binôme. Pour cela, vous allez constituer un emboitement de 20 cubes puis vous allez tracer la droite graduée correspondante. Vous lacez votre tour sur la feuille et vous tracez un trait horizontal tout le long de l'emboitement. Ensuite, vous marquerez les graduations correspondant à la longueur de chaque cube. Enfin, vous écrirez les nombres sous les graduations. »

Insister sur l'importance de réaliser ce travail à deux : par exemple, un élève tient la tour de cubes pendant que son camarade trace les graduations.

Circuler dans la classe pour aider les binômes éprouvant des difficultés.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Mise en commun
Collectif
5 min

Présenter quelques droites graduées tracées par les élèves et leur demander d'expliquer comment ils ont procédé. Montrer les graduations ainsi que les intervalles qui correspondent chacun à la longueur d'un cube.

Expliquer aux élèves qu'ils vont utiliser cet outil pour trouver le nombre de cubes de différentes tours. Constituer un emboitement d'une quinzaine de cubes, placer une droite graduée au tableau et placer les cubes sur la ligne : « J'aligne le début de ma suite de cubes avec le 0, puis je regarde sur quelle graduation se termine ma suite. C'est 15 ; il y a donc 15 cubes dans mon emboitement. » Entourer 15 et vérifier en dénombrant les cubes avec les élèves.

Placeholder pour Illustration : règle graduée de 0 à 20, 15 unités sont représentées en bleu.Illustration : règle graduée de 0 à 20, 15 unités sont représentées en bleu.

« Grâce à la droite graduée, nous avons pu trouver très rapidement combien il y avait de cubes dans l'emboitement que j'ai préparé. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Compter plus vite que l'éclair
En binômes
10 min

Proposer aux élèves d'utiliser l'outil fabriqué pour compter plus vite que l'éclair : « À deux, vous allez fabriquer un emboitement constitué du nombre de cubes de votre choix, en utilisant 20 cubes maximum. Tous les binômes poseront leurs cubes emboités sur leur bureau, puis ils circuleront dans la classe pour compter les cubes de différents emboitements, en utilisant l'outil. » Rappeler aux élèves qu'ils n'ont pas besoin de dénombrer les cubes, qu'il suffit d'aligner le premier cube avec le début de la droite puis de lire le nombre correspondant à l'extrémité du dernier cube.

Proposer aux élèves de consigner les nombres trouvés dans leur cahier de recherche. Durant cette phase, laisser les élèves circuler dans la classe pour tester leur droite graduée sur différentes suites de cubes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

6
Bilan collectif
Collectif
3 min

  • Bilan de l'activité
    • « Si vous avez réussi à trouver le nombre de cubes utilisés dans les emboitements à l'aide de la droite graduée, levez le pouce sur le cœur. »

  • Bilan mathématique
    • Afficher à nouveau la droite graduée, superposer une suite de cubes et demander aux élèves combien il y a de cubes dans la suite. Valider en dénombrant les cubes.

  • Bilan métacognitif
    • Demander aux élèves d'échanger à deux sur ce qu'ils ont appris, en chuchotant.

  • Synthèse en revenant à la cible
    • « Avec cette activité, nous avons découvert la droite graduée : elle permet de représenter les nombres sur une ligne. Les nombres sont placés régulièrement sur la droite : cela veut dire que l'espace entre chaque graduation est le même. Il représente une unité. » Montrer avec le doigt, comme lors de la construction de la droite.

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.