Problèmes équivalents à la recherche d'un tout

• Résoudre des problèmes de type transformation positive avec recherche de l'état final
• Résoudre des problèmes de type transformation négative avec recherche de l'état initial

Dans cette séquence, on s'intéresse à des problèmes de transformation positive et négative. Dans ces problèmes, on passe d'un état initial à un état final par une transformation : ces problèmes ont une dimension temporelle. Cependant, les problèmes de types transformation et partie-tout se schématisent et se résolvent de la même manière, il est donc nécessaire de faire le lien entre ces deux types de problèmes auprès des élèves.
Plus d'explications en

vidéo

.

1

Rappel des activités réalisées

Collectif

2 min

Demander aux élèves de raconter le problème de la tour. « Aujourd'hui, nous allons continuer à résoudre des problèmes. Nous allons chercher combien il y a d'objets en tout après avoir fait un ajout. Pour cela, jouer au jeu de la boite opaque. »

2

Exploration de la situation du premier problème

En binômes puis collectif

10 min

« Chaque joueur a 5 cubes. Le premier joueur met autant de cubes qu'il veut dans la boite. Il la donne au deuxième joueur en lui disant combien il y a de cubes. Le deuxième joueur ajoute des cubes en disant combien il en met. Puis vous cherchez ensemble combien il y a de cubes dans la boite. Lorsque vous pensez avoir trouvé, vous sortez les cubes pour vérifier. »
Laisser les élèves jouer à deux, puis organiser une mise en commun.

Après quelques minutes, faire réaliser l'activité à deux élèves devant la classe, en verbalisant leur action :
« On met 2 cubes dans la boite puis on en rajoute 5. »

Puis, demander à toute la classe : « Combien y a-t-il de cubes dans la boite ? Mettez-vous d'accord avec votre voisin. »

Mettre en commun les réponses ainsi que les procédures des élèves. On peut attendre les propositions suivantes :

• J'utilise mes doigts : 2 plus 5, ça fait 7. Il y a 7 cubes.
• J'imagine 2 cubes, puis 5 cubes : ça fait 7.
• Je sais que 2 + 5 = 7. Il y a donc 7 cubes dans la boite.

Refaire cette activité collectivement pour s'assurer de la compréhension de la situation par les élèves.

3

Découverte du premier problème et reformulation

Collectif

5 min

« À présent, nous allons essayer de continuer ce jeu sans vraiment mettre les jetons dans la boite. »
Lire le problème : « Il y a 5 cubes dans la boite. On en ajoute 3. Combien y a-t-il de cubes dans la boite maintenant ? »

Afficher l'image « Boite » au tableau. Écrire « 5 » dans la boite, puis « 3 » avec une flèche en direction de la boite.

Amener les élèves à reformuler le problème : « Pour que tout le monde comprenne bien, vous allez raconter à votre voisin l'histoire de ce problème. » Permettre aux élèves d'échanger à deux, puis interroger quelques binômes.

« Maintenant, vous allez dire à deux ce qu'on cherche, veut savoir. » L'objectif est que les élèves reformulent la question et se l'approprient : veiller à ce que tous aient compris ce qu'on cherche afin que tous puissent se lancer dans la résolution du problème.

4

Résolution du premier problème sur le fichier

5 min

Projeter la page 142 du fichier, sur laquelle figure le problème.
« Vous allez essayer de trouver tout seul la réponse à la question. Il faudra l'écrire dans votre fichier. Pour vous aider, vous pouvez prendre du matériel ou dessiner. Lorsque vous pensez avoir trouvé, vous écrivez la réponse, puis vous vous mettez d'accord avec votre voisin. » Relire le problème.

5

Mise en commun

Collectif

5 min

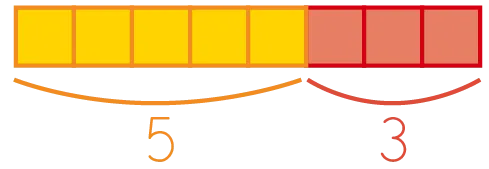
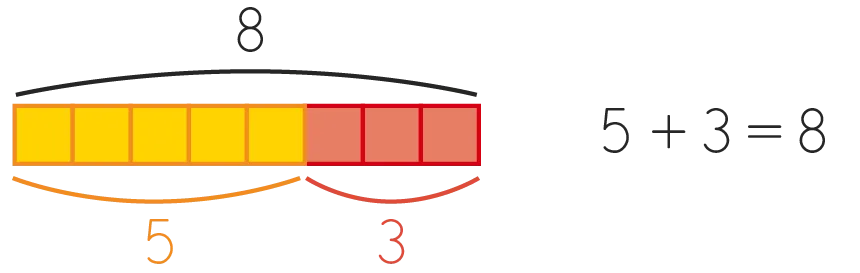
Afficher quelques productions d'élèves. Observer différentes représentations proposées par les élèves et leur demander d'expliquer leur procédure de résolution. Pour chaque proposition, demander au groupe-classe « Est-ce que cette réponse est possible ? » afin de les faire réfléchir à la vraisemblance du résultat proposé. On mettra ainsi en lumière qu'il n'est pas possible qu'il y ait moins de 5 cubes dans la boite. Utiliser le matériel pour valider collectivement la réponse proposée. Proposer une schématisation de la situation.

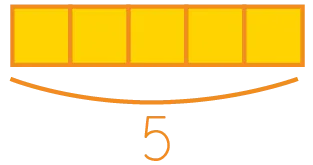
« Il y avait 5 cubes dans la boite. » Emboiter 5 cubes et écrire « 5 ». « J'en ajoute 3. » Emboiter 3 cubes d'une autre couleur et écrire « 3 ». « 5 cubes et 3 cubes, ça fait 8. Il y a 8 cubes en tout dans la boite. » Écrire « 8 » au-dessus de la tour et « 5 + 3 = 8 » à côté. « Quel est le point commun avec les problèmes que vous avez déjà résolus ? » Expliquer aux élèves que dans cette situation aussi on cherche combien il y a de cubes en tout. « Nous avions des cubes au début de l'histoire, puis on en a ajouté. On cherche combien on en a en tout à la fin de l'histoire. »

6

Résolution du second problème

Individuel

5 min

Projeter à nouveau la page 142 du fichier.
« Il y a 4 passagers dans le bus. 5 personnes les rejoignent. Combien y a-t-il de personnes dans le bus maintenant ? »
Laisser les élèves résoudre le problème dans leur fichier.

7

Bilan

Collectif

3 min

• Bilan de l'activité
« Si vous avez réussi à trouver la réponse au problème, levez le pouce sur le cœur. »


• Bilan mathématique
Mettre successivement 4, puis encore 4 cubes dans la boite. Demander aux élèves de montrer avec leurs doigts le nombre total de cubes obtenu.


• Bilan métacognitif
Demander aux élèves d'échanger à deux sur ce qu'ils ont appris.


• Synthèse en revenant à la cible
« Nous avons résolu des problèmes dans lesquels on cherche combien il y a d'objets en tout après un ajout. On peut les résoudre de la même façon que le problème de la tour. »