Chapitre 10
Activités
Découvrir le chapitre : Proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Histoire des maths
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Les proportions
L'approche que nous avons de nos jours de la proportionnalité est avant tout une approche fonctionnelle : tableaux de proportionnalité ou représentations graphiques. Cependant, avant cette approche, il est évident que l'on avait besoin d'utiliser ou de trouver des grandeurs proportionnelles. Euclide (environ 300 av. J.-C.) consacre tout le livre V de ses Éléments aux proportions et on peut encore aujourd'hui utiliser ses résultats. Avec les notations actuelles, voici une propriété que l'on peut y trouver : quatre nombres non nuls a, b, c et d définissent une
proportion lorsque \frac{a}{b}=\frac{c}{d}.
Dès lors que l'on a cette proportion, on a aussi, par exemple, les proportions suivantes : {\frac{a}{c}=\frac{b}{d}} , {\frac{b}{a}=\frac{d}{c}} , {\frac{a+b}{b}=\frac{c+d}{d}~,} a d=b c , \frac{a-b}{b}=\frac{c-d}{d} , \frac{a}{b}=\frac{a+c}{b+d} ou encore {\frac{a}{b}=\frac{a-c}{b-d}}.
Dès lors que l'on a cette proportion, on a aussi, par exemple, les proportions suivantes : {\frac{a}{c}=\frac{b}{d}} , {\frac{b}{a}=\frac{d}{c}} , {\frac{a+b}{b}=\frac{c+d}{d}~,} a d=b c , \frac{a-b}{b}=\frac{c-d}{d} , \frac{a}{b}=\frac{a+c}{b+d} ou encore {\frac{a}{b}=\frac{a-c}{b-d}}.
Au XIXe siècle, en reprenant les propositions du livre V des Éléments, le mathématicien Karl Weierstrass réussit à donner à l'analyse toute la rigueur dont elle avait besoin. Il a été le professeur de grands mathématiciens comme Georg Cantor, Felix Klein, Sophus Lie, Hermann Minkowski et Sofia Kovalevskaya.
En se servant des propriétés d'Euclide ci-dessus, trouver deux nombres dont la différence est 12 et le quotient \frac{11}{5}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 1Produits en croix
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Chez le fromager, 300 g de raclette coûtent 5,55 €. John en achète 420 g. On sait que le prix est proportionnel à la masse achetée.
| Masse de fromage en gramme | 300 | 1 | 200 | 420 |
|---|---|---|---|---|
| Prix en euro | 5,55 | x | y | z |
1
Calculer le prix x d'un gramme de fromage.2
Comment peut-on trouver le prix y de 200 g de fromage ?3
Calculer le prix z payé par John pour l'achat de son fromage.Bilan
Comment peut-on retrouver le prix de 420 g de fromage sans calculer le prix de
1 g de fromage, ni celui de 200 g ? Recopier et compléter cette égalité :
z=\frac{.... \times ....}{.... }.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 2Caractérisation graphique de la proportionnalité
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Pauline souhaiterait pratiquer de la zumba. Elle a trouvé trois clubs proposant chacun un tarif différent.
ZumbaFun
| Nombre de mois | 3 | 6 | 9 | 12 |
|---|---|---|---|---|
| Prix en € | 90 | 180 | 270 | 360 |
KaZumba
| Nombre de mois | 3 | 6 | 9 | 12 |
|---|---|---|---|---|
| Prix en € | 120 | 180 | 240 | 300 |
ZumbaFamily
| Nombre de mois | 3 | 6 | 9 | 12 |
|---|---|---|---|---|
| Prix en € | 120 | 240 | 360 | 450 |
1
Parmi ces trois tableaux, lequel est un tableau de proportionnalité ? Justifier.2
Placer dans un même repère les points associés à chacun des trois tableaux. On indiquera en abscisse (sur l'axe horizontal) le nombre de mois en prenant 1 cm pour un mois et en ordonnée (sur l'axe vertical) le prix en euro en prenant
1 cm pour 30 €.
GeoGebra
Bilan
Quelles semblent être les conditions pour qu'un graphique représente une situation de proportionnalité ?
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Activité 3Agrandissement et réduction
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Soit \text{ABCD} un rectangle de longueur 4,5 cm et de largeur 3 cm.
1
Parmi ces cinq autres rectangles (toutes les mesures sont en cm), lesquels ont
des dimensions proportionnelles à celles de \text{ABCD} ? Justifier la réponse.
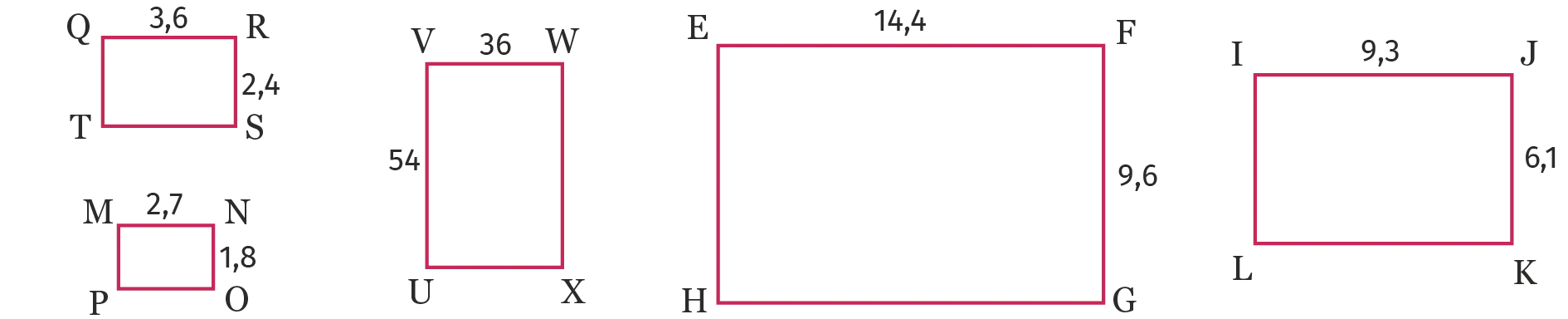
2
On dit que l'on effectue un agrandissement ou une réduction d'une figure lorsque l'on multiplie toutes les longueurs d'une figure par un même nombre k > 0. En revanche, les mesures des angles restent inchangées. Parmi les rectangles précédents, lesquels sont un agrandissement ou une réduction du rectangle \text{ABCD} ? Indiquer la valeur de k pour chacun de ces rectangles.3
Que se passerait-il si les longueurs de \text{ABCD} étaient multipliées par un coefficient k égal à 1 ?Bilan
Comment peut-on reconnaître un agrandissement ou une réduction à partir du coefficient multiplicateur k appliqué à la figure initiale ?Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
