Nos classiques

Guide CP-Maths

Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
I
Présentation
II
Liaison grande section - CP
Période 1
Période 2
13- Associer des heures à des moments de la journée
Grandeurs et mesuresp. 76-77
14- Repérer des motifs et les compléter
Numérationp. 78-80
15- Découvrir la soustraction
Numérationp. 81-84
16- Nombre précédent et nombre suivant
Numérationp. 85-86
17- Comparer des quantités jusqu’à 99
Numérationp. 87-90
18- Additionner trois nombres
Calculp. 91-93
19- Compter de 2 en 2 jusqu’à 30
Numérationp. 94-95
20- Comparer des objets et des segments
Grandeurs et mesuresp. 96-99
21- Faire des échanges dizaines-unités
Numérationp. 100-103
22- Situer des objets dans l’espace et sur une feuille
Géométriep. 104-106
23- Soustraire des nombres
Calculp. 107-109
24- Suite écrite des nombres jusqu’à 59
Numérationp. 110-111
25- Comparer et ordonner des nombres jusqu’à 59
Numérationp. 112-114
26- Reconnaitre et nommer les solides usuels
Géométriep. 115-117
Problèmes de type partie-tout : recherche d’une partie
Problèmesp. 118-120
Problèmes équivalents à la recherche d’une partie
Problèmesp. 121-123
Problèmes inventés
Problèmesp. 124-125
Problèmes en plein air
Problèmesp. 126-127
Période 3
Période 4
Période 5
Annexes
Calcul
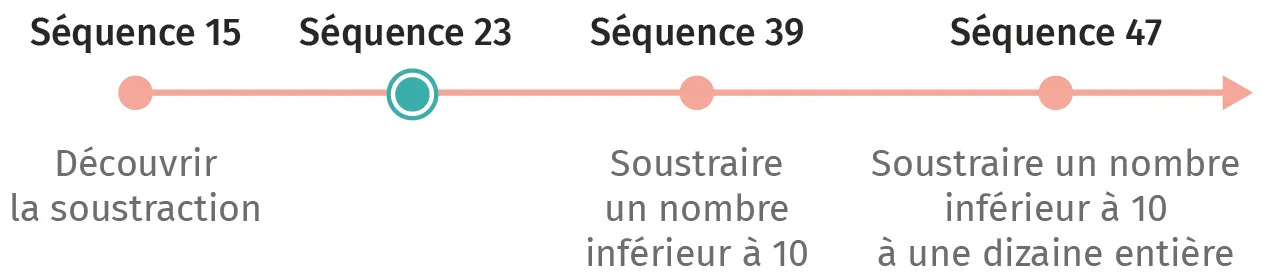
Séquence 23

Soustraire des nombres

Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Placeholder pour Schéma apprentissage soustraction: découverte, soustraction de nombres inférieurs à 10, puis soustraction d'un nombre inférieur à 10 à une dizaine.Schéma apprentissage soustraction: découverte, soustraction de nombres inférieurs à 10, puis soustraction d'un nombre inférieur à 10 à une dizaine.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Objectif de la séquence

  • Soustraire des nombres inférieurs à 10
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Conseil didactique

Dans la séquence 15, les élèves ont découvert les deux premiers sens de la soustraction le sens « enlever » et le sens « pour aller à », c'est-à-dire rechercher le complément. Dans cette séquence, ils explorent son troisième sens : la recherche de la différence, c'est-à-dire de l'écart entre deux valeurs. On s'appuiera à nouveau sur les tours de cubes pour aider les élèves à faire le lien entre les différentes situations soustractives rencontrées.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
SÉANCE 2
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Séance 1
60 min
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Problèmes du jour
Individuel
10 min

Problèmes additifs : recherche du tout

Problème 1

Leïla achète 13 caramels et 5 sucettes.
Combien de bonbons a-t-elle achetés en tout ?
Retrouvez ce problème au format
numérique
.

Problème 2

À midi, 9 personnes étaient venues à la bibliothèque. Dans l'après-midi, 7 personnes de plus sont venues à la bibliothèque.
Combien de personnes sont venues à la bibliothèque aujourd'hui ?
Retrouvez ce problème au format
numérique
.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Rituel de calcul
Collectif
10 min

Ajouter trois nombres inférieurs à 10

Énoncer une addition à trois nombres. Les élèves écrivent le calcul et son résultat sur leur ardoise. Valider en écrivant l'addition au tableau et modéliser le résultat sur la droite graduée. Répéter cinq fois.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

Apprentissage
40 min

Objectif de la séance
  • Soustraire en utilisant la droite graduée
Matériel de la séance
  • Une vingtaine de cubes par binôme
  • Un jeu de cartes « nombre » de 1 à 10 par binôme (matériel détachable)
  • Fichier élève p. 52
  • Ressources numériques à projeter
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

1
Entrée dans l'activité
Collectif
2 min

Présenter aux élèves une tour de 9 cubes à l'aide de l'outil « Droite graduée » ou avec du matériel.

Leur demander : « Je voudrais rétrécir ma tour pour qu'elle soit seulement constituée de 5 cubes. Combien de cubes dois-je enlever ? »
Laisser les élèves réfléchir, puis recueillir leurs propositions et les valider en écrivant la soustraction « 9-5 = 4 » et en rétrécissant la tour.

« Aujourd'hui, nous allons poursuivre notre travail sur le sens de la soustraction, et continuer à écrire et effectuer des soustractions. »
Placeholder pour Illustration : étoile jaune souriante tenant une cible avec une flèche au centre.Illustration : étoile jaune souriante tenant une cible avec une flèche au centre.
Découvrir le sens de la soustraction comme recherche de la différence.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

2
Différence entre deux tours
Collectif
10 min

Présenter deux tours de cubes aux élèves, l'une constituée de 10 cubes et l'autre de 6.

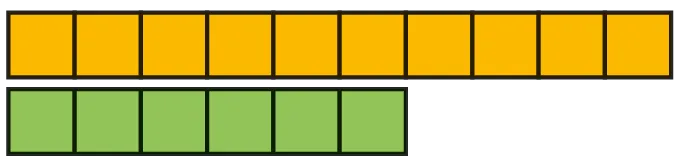
Placeholder pour Graphique: comparaison visuelle de données avec deux bandes de rectangles, une jaune et une verte, illustrant une différence quantitative.Graphique: comparaison visuelle de données avec deux bandes de rectangles, une jaune et une verte, illustrant une différence quantitative.

Demander aux élèves d'indiquer quelle est la tour la plus haute, puis expliquer : « Je voudrais connaitre la différence entre ces deux tours. Je vois que cette tour comporte 6 cubes, et que celle-ci en comporte 10 : il y a donc 4 cubes de différence (entourer les cubes). En effet, 6 + 4 = 10. On peut dire que la différence entre 10 et 6 est 4. Cela peut s'écrire avec une soustraction (écrire « 10-6 = 4 »). Pour trouver la réponse, on peut s'appuyer sur les décompositions des nombres. »

Organiser un temps d'appropriation en piochant deux cartes, en constituant les tours associées, puis en faisant chercher aux élèves la différence entre ces tours. Écrire la soustraction correspondante, et verbaliser en indiquant la différence entre les tours. Entourer les cubes de différence au tableau.

« Lorsqu'on cherche la différence entre deux tours, on cherche l'écart qu'il y a entre les deux. Cela revient à chercher combien de cubes il faut enlever à la plus grande tour pour qu'elle ait le même nombre de cubes que la plus petite, ou à chercher combien de cubes il faut ajouter à la plus petite pour qu'elle ait le même nombre de cubes que la plus grande. Cela s'appelle la différence. On peut aussi dire l'écart. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

3
Problèmes de cubes en binômes
En binômes
10 min

Chaque binôme dispose d'une vingtaine de cubes et d'un jeu de cartes. Dans cette étape, constituer des binômes homogènes pour permettre à tous les élèves de s'entraîner à leur rythme.

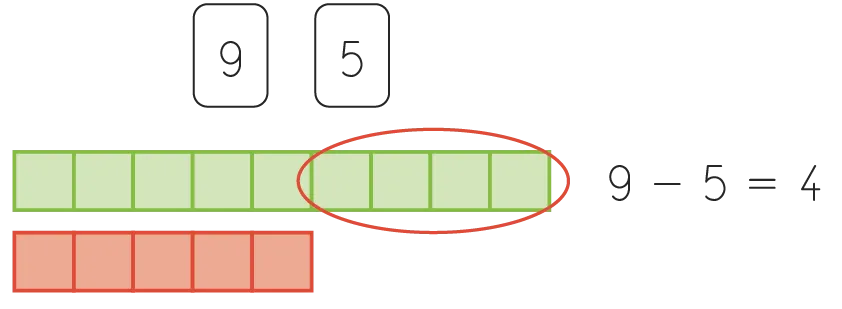
Chaque élève pioche une carte nombre, puis constitue la tour de cubes associée. Les élèves comparent ensuite leur tour en cherchant à modéliser la différence par une soustraction. Il est possible que les élèves trouvent directement la réponse à la question : il est pour autant essentiel qu'ils écrivent la soustraction associée.

Organiser une mise en commun : piocher deux cartes, constituer les tours de cubes et écrire la différence sous la forme d'une soustraction.

Placeholder pour Illustration graphique: soustraction 9-5=4. Représentation visuelle avec blocs pour l'apprentissage des mathématiques.Illustration graphique: soustraction 9-5=4. Représentation visuelle avec blocs pour l'apprentissage des mathématiques.

Verbaliser de manière à faire le lien entre les différentes situations soustractives découvertes lors de la séquence 15 et la recherche de la différence : « La tour de 5 cubes est plus petite que la tour de 9 cubes. Je cherche la différence entre 5 et 9 : c'est 4. En effet, je sais que 5 + 4 = 9. Je peux écrire une soustraction : 9 - 5 = 4. »
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

4
Entrainement individuel sur le fichier
Individuel
15 min

Projeter la page 52 du fichier et donner les consignes.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.

5
Bilan
Collectif
3 min

  • Bilan de l'activité
    • « Si vous avez réussi à trouver la différence entre les tours que vous avez fabriquées, levez le pouce sur le cœur. »

  • Bilan mathématique
    • Piocher deux cartes et les accrocher au tableau, par exemple « 6 » et « 4 ». Demander aux élèves d'imaginer les deux tours et d'écrire la différence entre ces tours avec une soustraction. Verbaliser : « Chercher la différence entre ces tours, cela revient à chercher combien de cubes il manque pour que la plus petite ait la taille de la plus grande ou combien de cubes il faut enlever pour que la plus grande ait la taille de la petite. C'est l'écart entre les deux tours. Ici, on sait que 4 + 2 = 6, donc 6-4 = 2. Il y a 2 cubes de différence entre ces deux tours. »

  • Bilan métacognitif
    • Demander aux élèves d'échanger à deux sur ce qu'ils ont appris, en chuchotant.

  • Synthèse en revenant à la cible
    • « Ce travail sert à apprendre à soustraire. Vous avez écrit et effectué des soustractions en cherchant la différence entre deux tours. »

Une erreur sur la page ? Une idée à proposer ?

Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.

j'ai une idée !

Oups, une coquille

Utilisation des cookies
Lors de votre navigation sur ce site, des cookies nécessaires au bon fonctionnement et exemptés de consentement sont déposés.