Rejoignez la communauté !
Co-construisez les ressources dont vous avez besoin et partagez votre expertise pédagogique.
Automatismes
Ch. 1
Statistiques à une variable
Ch. 2
Fluctuations d'une fréquence et probabilités
Ch. 3
Résolution d'un problème du premier degré
Ch. 4
Représentation et variations d'une fonction
Ch. 5
Fonctions affines, fonction carré
Ch. 6
Calculs commerciaux et financiers
Ch. 7
Géométrie
Fiches méthodes
Automatisme 10
Transformation de formules, expression d'une variable en fonction des autres
10 professeurs ont participé à cette page
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rituel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez tous les rituels sur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Exprimer \mathrm{L} en fonction de x.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Exprimer x en fonction de \mathrm{L}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
La vitesse moyenne se calcule à l'aide de la formule v=\frac{d}{t}. Exprimer la distance d en fonction de la vitesse v et du temps t.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
En utilisant la formule \mathrm{U}=\mathrm{R} \times \mathrm{I}, calculer \mathrm{R},
en \Omega, avec \mathrm{U}=12 V et \mathrm{I}=0,5 A.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Sachant que la fréquence f d'un signal est de 50 Hz, calculer la période \mathrm{T}, en seconde, de ce signal en utilisant la formule f=\frac{1}{T}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
J'apprends
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exprimer une variable en fonction des autres consiste à isoler cette variable afin de pouvoir la calculer. Il est possible de transformer une formule en mettant en œuvre les méthodes de résolution des équations.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
1
Le poids d'un objet est de 5 N.
Calculer la masse de cet objet à l'aide de la formule \text{\red{P}} = \blue{m} \times g. On prendra g = 10 N/kg.
Pour exprimer \blue{m} en fonction de \text{\red{P}}, on doit isoler \blue{m}. Pour cela, on divise \text{\red{P}} par g.
\blue{m}=\frac{\mathrm{\red{P}}}{g}=\frac{5}{10}=0,5 kg
Retrouvez une animation en démonstration
Le zoom est accessible dans la version Premium.
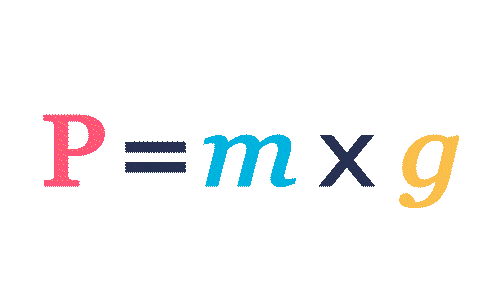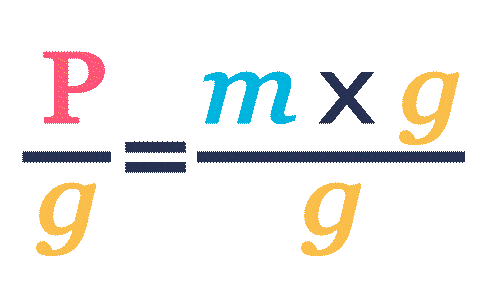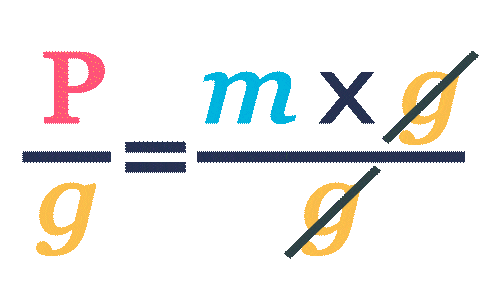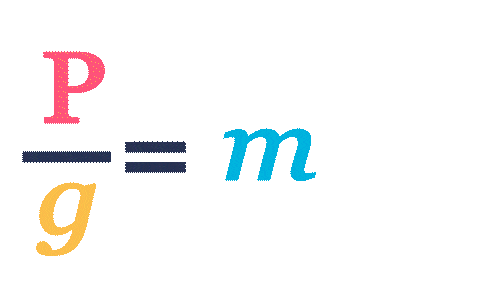
2
Exprimer le rayon \mathrm{\blue{R}} d'un cercle en fonction de son périmètre \mathcal{\red{P}}.
Le périmètre \mathcal{\red{P}} d'un cercle de rayon \mathrm{\blue{R}} est donné par la relation \mathcal{\red{P}}=2 \times \pi \times \mathrm{\blue{R}}.
Pour exprimer \mathrm{\blue{R}} en fonction de \mathcal{\red{P}}, on divise \mathcal{\red{P}} par 2 \times \pi.
\mathrm{\blue{R}}=\frac{\mathcal{\red{P}}}{2 \times \pi}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraîne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Le schéma ci-dessous revient à dire que \mathrm{L}=x+10. Exprimer x en fonction de \mathrm{L}.
Le zoom est accessible dans la version Premium.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
La relation entre la température \mathrm{T}_{\mathrm{K}} en Kelvin et la température \mathrm{T}_{\mathrm{C}} en degré Celsius est la suivante : \mathrm{T}_{\mathrm{K}}=\mathrm{T}_{\mathrm{C}}+273,15. Exprimer \mathrm{T}_{\mathrm{C}} en fonction de \mathrm{T}_{\mathrm{K}}.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Exprimer \mathrm{U}_{\mathrm{eff}} en fonction de \mathrm{U}_{\max} à partir
de la formule \mathrm{U}_{\max }=\mathrm{U}_{\mathrm{eff}} \times \sqrt{2}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Pour calculer une longueur d'onde, on
utilise la formule suivante : \lambda=c \times \text{T}.
Exprimer \text{T} en fonction de \lambda et c.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Un cycliste a parcouru 50 kilomètres en
4 heures.
Calculer sa vitesse moyenne en km/h à partir de la formule d=v \times t.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
6
La concentration massique d'un soluté est \mathrm{C}_m=0,8 g/L.
Calculer la masse, en gramme, du soluté dissous dans 2,5 L de solution à partir de la formule \mathrm{C}_m=\frac{m}{\mathrm{~V}}.
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
Oups, une coquille
j'ai une idée !
Nous préparons votre pageNous vous offrons 5 essais
YolèneÉmilieJean-PaulFatimaSarah