Automatisme 16
Utilisation des procédures de résolution graphique d'équations
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Rituel
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Retrouvez tous les rituels sur
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Déterminer l'abscisse du point d'intersection des droites d_1 et d_2.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Déterminer l'abscisse
du point d'intersection de la
droite d_2 et de la courbe \cal C.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
3
Soit f et g les fonctions représentées respectivement par les courbes \cal{C}_f et \cal{C}_g.
Déterminer l'abscisse des points d'intersection des courbes \cal{C}_f et \cal{C}_g.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
4
Soit f et g les fonctions définies par f(x)=x+1 et g(x)=2 x-1.
Résoudre graphiquement l'équation x+1=2 x-1.
Résoudre graphiquement l'équation x+1=2 x-1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
5
Soit f et g les fonctions définies par f(x)=x^2-x+1 et g(x)=x+1.
Résoudre graphiquement les équations x+1=0 et x^2-x+1=x+1.
Résoudre graphiquement les équations x+1=0 et x^2-x+1=x+1.
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
J'apprends
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Équation de la forme \bm{f(x)=0}
Équation de la forme \bm{f(x)=g(x)}
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Exemples
1
La fonction f définie par f(x)=x^2-4 est représentée graphiquement ci-dessous.
Résoudre graphiquement l'équation f(x)=0.
Les solutions de l'équation f(x)=0, c'est-à-dire x^2-4=0, sont x=\red{-2} et x=\red{2}.
Retrouvez une animation en démonstration
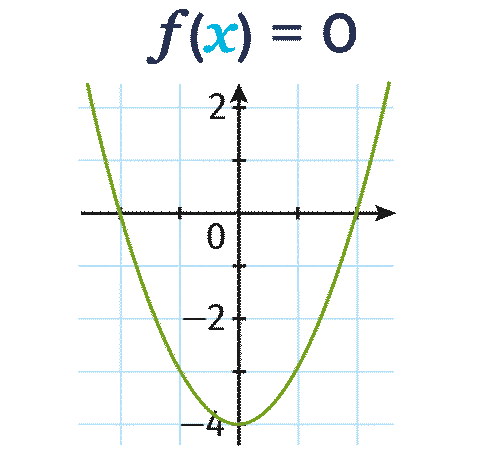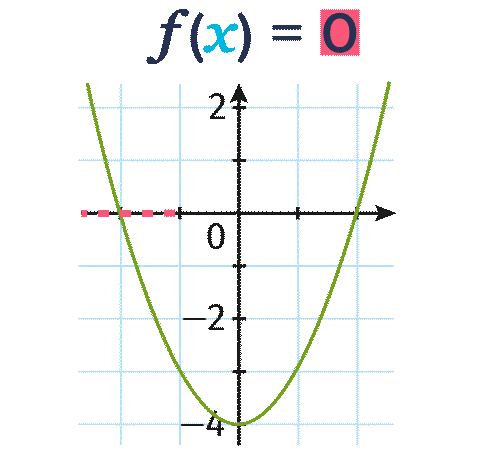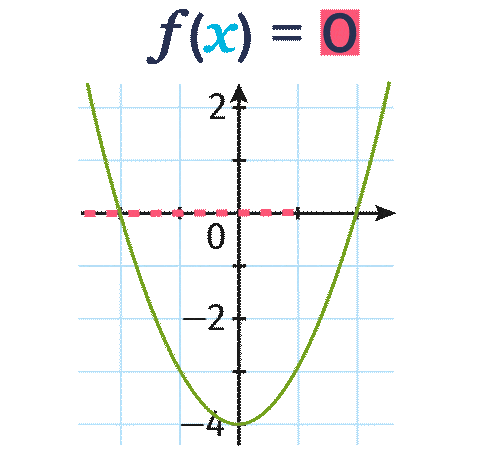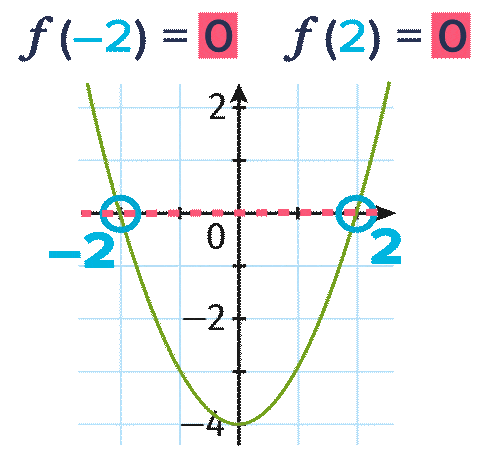
2
Les fonctions f et g définies par f(x)=2 x+1 et g(x)=-3 x+6 sont représentées graphiquement ci-dessous.
Résoudre graphiquement l'équation f(x)=g(x).
La solution de l'équation f(x)=g(x), c'est-à-dire 2 x+1=-3 x+6, est x=\red{1}.
Retrouvez une animation en démonstration
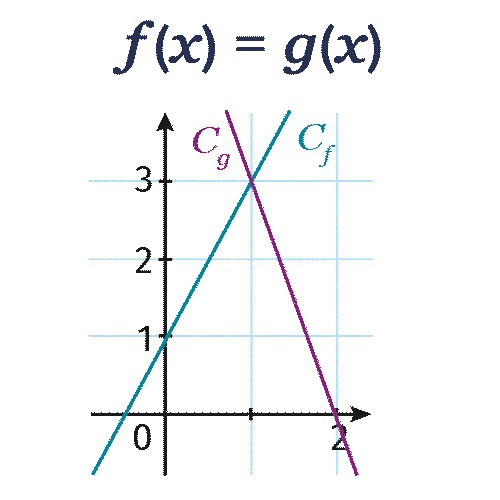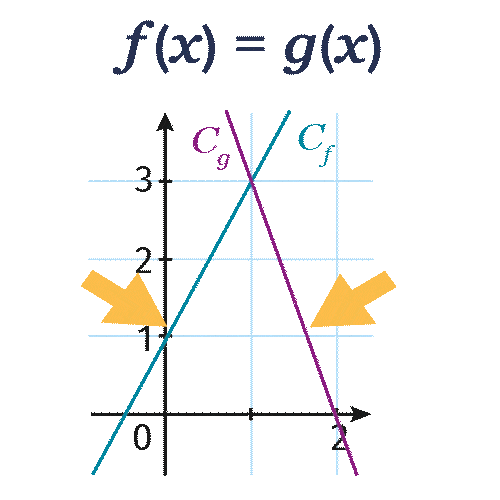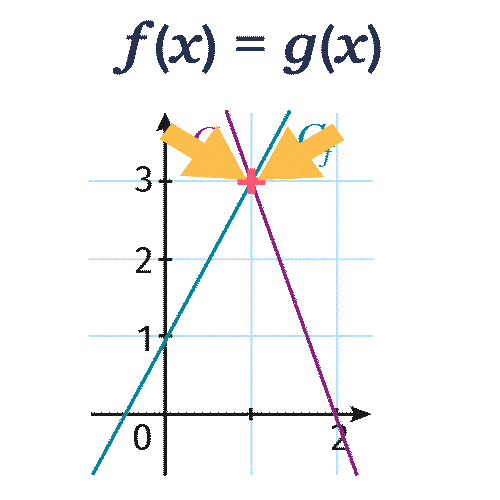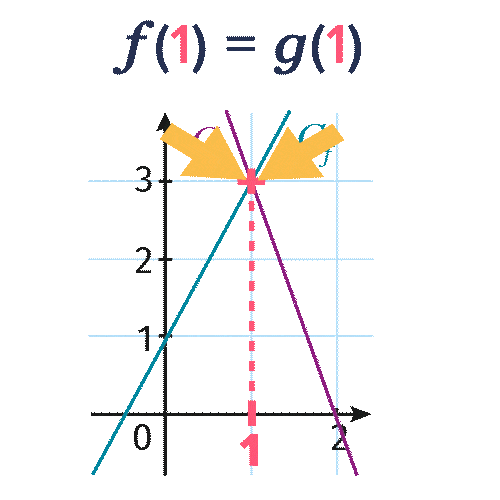
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
Je m'entraîne
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
1
Les fonctions f et g définies par f(x)=2 x^2-1 et g(x)=-2 x-1 sont représentées graphiquement ci-dessous.
Résoudre graphiquement les équations suivantes.
1.
-2 x-1=3
2.
2 x^2-1=1
3.
g(x)=-1
4.
2 x^2-1=-2 x-1
Ressource affichée de l'autre côté.
Faites défiler pour voir la suite.
Faites défiler pour voir la suite.
2
Les fonctions f et g définies par f(x)=x+2 et g(x)=-2 x+2, et la droite d'équation y = 4 sont représentées graphiquement ci-dessous.
Résoudre graphiquement les équations suivantes.
1.
f(x)=0
2.
g(x)=0
3.
-2 x+2=4
4.
f(x)=g(x)
Une erreur sur la page ? Une idée à proposer ?
Nos manuels sont collaboratifs, n'hésitez pas à nous en faire part.
j'ai une idée !
Oups, une coquille
